题目内容
已知函数![]()
(Ⅰ) 求函数![]() 的极值;
的极值;
(Ⅱ) 求证:当![]() 时,
时,![]()
(Ⅲ) 如果![]() ,且
,且![]() ,求证:
,求证:![]()
解:⑴∵![]() =
=![]() ,∴
,∴![]() =
=![]() . (2分)
. (2分)
令![]() =0,解得
=0,解得![]() .
.
|
|
| 1 |
|
|
| + | 0 | - |
|
| ↗ | 极大值 | ↘ |
(3分)
∴当![]() 时,
时,![]() 取得极大值
取得极大值![]() =
=![]() . (4分)
. (4分)
⑵证明:![]() ,则
,则
![]() =
=![]() . (6分)
. (6分)
当![]() 时,
时,![]() <0,
<0,![]() >2,从而
>2,从而![]() <0,
<0,
∴![]() >0,
>0,![]() 在
在![]() 是增函数.
是增函数.
![]() (8分)
(8分)
⑶证明:∵![]() 在
在![]() 内是增函数,在
内是增函数,在![]() 内是减函数.
内是减函数.
∴当![]() ,且
,且![]() 时,
时,![]() 、
、![]() 不可能在同一单调区间内.
不可能在同一单调区间内.
∴![]() ,
,
由⑵的结论知![]() 时,
时,![]() >0,∴
>0,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() (12分)
(12分)

练习册系列答案
相关题目
 .
. 上的最大值和最小值.
上的最大值和最小值. .
. 成立的
成立的 的取值范围;
的取值范围; 时,求函数
时,求函数 的值域.
的值域. .
. 的单调区间;
的单调区间; 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间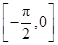 上的最小值和最大值.
上的最小值和最大值. .
. 的最小正周期及最值;
的最小正周期及最值; ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.