题目内容
7、已知三条相交于一点的线段PA，PB，PC两两垂直，且A，B，C在同一平面内，P在平面ABC外，PH⊥平面ABC于H，则垂足H是△ABC的（ ）
分析：本题利用直接法解决．根据PA，PB，PC两两垂直得线面垂直，最后由线面垂直可证明线线垂直，得垂足H是△ABC的垂心．从而选出答案．
解答：解：
∵PH⊥平面ABC于H，
∴PH⊥BC，
又PA⊥平面PBC，
∴PA⊥BC，
∴BC⊥平面PAH，
∴BC⊥AH，即AH是三角形ABC的高线，
同理，BH、CH也是三角形ABC的高线，
∴垂足H是△ABC的垂心．
故选D．
∵PH⊥平面ABC于H，∴PH⊥BC，
又PA⊥平面PBC，
∴PA⊥BC，
∴BC⊥平面PAH，
∴BC⊥AH，即AH是三角形ABC的高线，
同理，BH、CH也是三角形ABC的高线，
∴垂足H是△ABC的垂心．
故选D．
点评：本题主要考查了三角形五心，以及空间几何体的概念、空间想象力，属于基础题．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
(其中
)，那么
的位置关系是 
，
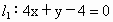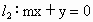及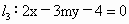
，求m分别满足下列条件时的值：