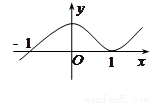题目内容
已知函数
的图象如图所示，则f（x）=（ ）A．
B．
C．
D．
【答案】分析：先由图象确定A、B、T，再由T确定ω，最后通过特殊点（最高点或最低点）确定φ，进而明确A，则问题解决．
解答：解：由图象得A=±
=±2，B=4，
=
=π，
则T=4π，ω=
=
，
此时f（x）=±2sin（
+φ）+4，
将特殊点（
，6）代入解析式有sin（
+φ）=±1，
又0＜φ＜
，则φ=
，A=2，
所以f（x）=2sin（
）+4．
故选C．
点评：本题考查由三角函数部分图象信息求函数解析式的基本方法．
解答：解：由图象得A=±
=±2，B=4，==π，则T=4π，ω=
=，此时f（x）=±2sin（
+φ）+4，将特殊点（
，6）代入解析式有sin（+φ）=±1，又0＜φ＜
，则φ=，A=2，所以f（x）=2sin（
）+4．故选C．
点评：本题考查由三角函数部分图象信息求函数解析式的基本方法．
练习册系列答案
相关题目
已知函数的图象如图所示，则其函数解析式可能是（ ）
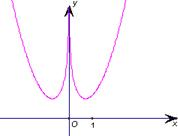
| A、f（x）=x2+ln|x| | B、f（x）=x2-ln|x| | C、f（x）=x+ln|x| | D、f（x）=x-ln|x| |
的图象如图所示，
，则
．
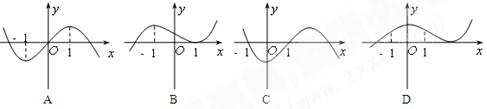
已知函数
的图象如图所示，则
满足的关系是（ ）
B．
D．
的图象如图所示．
的解析式；
，且方程
有两个不同的实数根，求实数
的取值范围和这两个根的和；
中，若
，求
的取值范围．
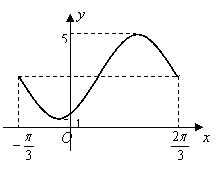
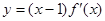的图象如图所示，其中
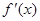为函数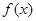
的导函数，则
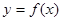的大致图象是( )
