题目内容
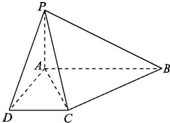（2009•台州一模）已知四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AD=CD=1，∠BAD=120°，PA=| 3 |
（Ⅰ）求证：BC⊥平面PAC；
（Ⅱ）求直线PC与平面PAB所成的角的正弦值．
分析：本题考查空间中的直线与平面的垂直关系，考查直线与平面所成的角．证明直线与平面垂直的关键是证明直线与平面内的两条相交直线垂直；求线面角的关键是得出直线在平面内的射影．（I）利用PA⊥底面ABCD，与已知得PA⊥BC及BC⊥AC，因此可证得BC⊥平面PAC；（Ⅱ）利用平面PAB⊥底面ABCD，作CE垂直AB，得CE⊥面PAB，直线PC与平面PAB所成的角为∠EPC，求出即可．
解答：
解：（Ⅰ）证明：∵PA⊥底面ABCD，BC?面ABCD
∴PA⊥BC，∵∠ACB=90°
∴BC⊥AC，又PA∩AC=A，
∴BC⊥平面PAC；
（Ⅱ）过C作CE⊥AB于E，连接PE．
∵PA⊥底面ABCD，PA?面PAB，∴面PAB⊥面ABCD，且面PAB∩面ABCD=AB，
∴CE⊥面PAB，
∴PE是PC在面PAB内的射影，∠EPC为直线PC与平面PAB所成的角．
∵AD=CD=1，∠ADC=60°．△ACD 为正三角形，∴AC=1，
PC=
=2，在直角三角形ACB中，∠BAC=60，AB=2，BC=
．又CE•AB=AC•BC，解得CE=
∴sin∠EPC=
=
．
解：（Ⅰ）证明：∵PA⊥底面ABCD，BC?面ABCD∴PA⊥BC，∵∠ACB=90°
∴BC⊥AC，又PA∩AC=A，
∴BC⊥平面PAC；
（Ⅱ）过C作CE⊥AB于E，连接PE．
∵PA⊥底面ABCD，PA?面PAB，∴面PAB⊥面ABCD，且面PAB∩面ABCD=AB，
∴CE⊥面PAB，
∴PE是PC在面PAB内的射影，∠EPC为直线PC与平面PAB所成的角．
∵AD=CD=1，∠ADC=60°．△ACD 为正三角形，∴AC=1，
PC=
| PA2+AC2 |
| 3 |
| ||
| 2 |
∴sin∠EPC=
| EC |
| PC |
| ||
| 4 |
点评：本题考查空间直线和平面垂直关系的判定，线面角的大小求解．立体几何的证明问题，得分容易，但得满分不易，主要原因是在运用综合法证明问题时，说理不充分，逻辑关系不严密，这就要求在解决这类问题时，一定要细心，做到步步有理由，环环相扣，不跳步．
练习册系列答案
期末集结号系列答案
相关题目
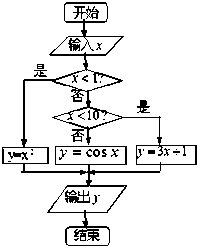（2009•台州一模）根据右边程序框图，若输出y的值是4，则输入的实数x=