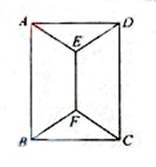
题目内容
.如图：用四种不同颜色给图中的ABCDEF六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共有 种．（用数字作答）
264．分两类讨论：第一类，用
到3种颜色，先给A\B\C三点涂色，因A、B、C两两相邻，所以颜色互不相同，有
种涂法，再给D．E．F涂色，因A与D，B与E，C与F颜色不同，故有2种，由乘法原理得
；第二类， 4种颜色都用到，先给 A． B．C三点涂色，有种涂法，再给D．E．F涂色，因为D．E．F中必有一点用到第4种颜色
，所以另外两点用到A．B．C三点所用颜色中的两种
，此时涂法确定，由乘法原理得
．所以共有+=264种．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
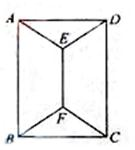11、如图，用四种不同颜色给图中的A，B，C，D，E，F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法用（ ）
