题目内容
若A点坐标为(1,1),F2是椭圆 +
+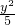 =1的右焦点,点P是椭圆的动点,则|PA|+|PF2|的最小值是________.
=1的右焦点,点P是椭圆的动点,则|PA|+|PF2|的最小值是________.
6-
分析:由椭圆的定义结合三角形的性质,即可求出表达式的最小值.
解答: 解:因为椭圆
解:因为椭圆 +
+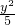 =1的a=3,c=2,所以F1(-2,0),
=1的a=3,c=2,所以F1(-2,0),
|F1A|= =
=
由椭圆的定义可知|PF1|+|PF2|=2a,|PF2|+|PA|+|F1A|≥|PF1|+|PF2|
∴|PF2|+|PA|≥|PF1|+|PF2|-|F1A|=6- ,所以有最小值6-
,所以有最小值6- ,
,
故答案为:6- .
.
点评:本题考查了椭圆的标准方程的意义,椭圆定义的应用,椭圆的几何性质,利用均值定理和函数求最值的方法.

分析:由椭圆的定义结合三角形的性质,即可求出表达式的最小值.
解答:
 解:因为椭圆
解:因为椭圆 +
+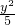 =1的a=3,c=2,所以F1(-2,0),
=1的a=3,c=2,所以F1(-2,0),|F1A|=
 =
=
由椭圆的定义可知|PF1|+|PF2|=2a,|PF2|+|PA|+|F1A|≥|PF1|+|PF2|
∴|PF2|+|PA|≥|PF1|+|PF2|-|F1A|=6-
 ,所以有最小值6-
,所以有最小值6- ,
,故答案为:6-
 .
.点评:本题考查了椭圆的标准方程的意义,椭圆定义的应用,椭圆的几何性质,利用均值定理和函数求最值的方法.

练习册系列答案
相关题目
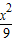 +
+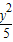 =1的右焦点,点P是椭圆的动点,则|PA|+|PF2|的最小值是 .
=1的右焦点,点P是椭圆的动点,则|PA|+|PF2|的最小值是 .