题目内容
17．已知定义在R上的函数y=f（x）与y=g（x），其图象如图所示，则对任意的实数a，方程g[f（x）]=a根的个数不可能为（ ）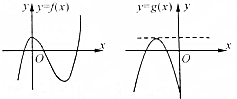
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 由f[g（x）]=0得，g（x）=x1，x2，x3，且x1＜0，x3＞x2 ＞0，分类讨论得出结论．
解答 解：由f[g（x）]=0得，g（x）=x1，x2，x3，且x1＜0，x3＞x2 ＞0；
g（x）=x1有且仅有两个解，
g（x）=x2可能有两个解、一个解，
g（x）=x3 解可能有两个解、一个解、没有解，
故方程f[g（x）]=0可能有6个解、5个解，4个解，绝不会是7个解的，
故选：D．
点评 本题考查了复合函数的应用及数形结合的思想应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
7．
执行如图所示的程序框图，则输出的n=（ ）
执行如图所示的程序框图，则输出的n=（ ）| A． | 63 | B． | 66 | C． | -93 | D． | -69 |
如图表示的是求首项为-41，公差为2的等差数列前n项和的最小值的程序框图，如果?②中填a=a+2，则①?可填写a＞0．
5．命题“?a∈[0，+∞），sina＞a”的否定形式是（ ）
| A． | ?a∈[0，+∞），sina≤a | B． | ?a∈[0，+∞），sina≤a | C． | ?a∈（-∞，0），sina≤a | D． | ?a∈（-∞，0），sina＞a |
7．在?ABCD中，已知$\overrightarrow{AC}$=（-4，2），$\overrightarrow{BD}$=（2，-6），那么|2$\overrightarrow{AB}$+$\overrightarrow{AD}$|=（ ）
| A． | 5$\sqrt{5}$ | B． | 2$\sqrt{5}$ | C． | 2$\sqrt{10}$ | D． | $\sqrt{85}$ |