题目内容
已知函数f(x)=ax2+3x+b(a<0,a、b∈R).设关于x的方程f(x)=0的两个实根分别为α、β
(1)若|α-β|=1,求a、b的关系式;
(2)若a、b均为负整数,且|α-β|=1,求f(x)的解析式;
(3)在(2)的条件下,若方程f(x)=(2m+2)x+2m+4至少有一个正根,求实数m的取值范围.
(1)若|α-β|=1,求a、b的关系式;
(2)若a、b均为负整数,且|α-β|=1,求f(x)的解析式;
(3)在(2)的条件下,若方程f(x)=(2m+2)x+2m+4至少有一个正根,求实数m的取值范围.
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:(1)利用根与系数之间的关系,结合条件|α-β|=1,即可求a、b的关系式;
(2)根据a、b均为负整数,且|α-β|=1,解方程组即可求f(x)的解析式;
(3)根据一元二次方程函数根的分布,建立条件关系即可得到结论.
(2)根据a、b均为负整数,且|α-β|=1,解方程组即可求f(x)的解析式;
(3)根据一元二次方程函数根的分布,建立条件关系即可得到结论.
解答:
解:(1)由题意可得α、β是ax2+3x+b=0 的两个根,
∴
,
∵|α-β|=1,∴|α-β|2=|α+β|2-4αβ=1,
即a2+4ab=9,(a<0).
(2)由(1)知a(a+4b)=9且a,b均为负整数,
故
或
(舍)或
(舍),
解得a=-1,b=-2,
∴f(x)=-x2+4x-2.
(3)方程f(x)=(2m+2)x+2m+4,
即x2+(2m-2)x+2m+6=0,
方程至少有一个正根,有三种可能:
①有两个正根,此时可得
,即
,
∴-3<m≤-1,
②有一个正根,一个负根,此时可得f(0)<0,得m<-3,
③有一个正根,另一根为零,此时可得
,
即
,
综合上述三种情况的m≤-1.
∴
|
∵|α-β|=1,∴|α-β|2=|α+β|2-4αβ=1,
即a2+4ab=9,(a<0).
(2)由(1)知a(a+4b)=9且a,b均为负整数,
故
|
|
|
解得a=-1,b=-2,
∴f(x)=-x2+4x-2.
(3)方程f(x)=(2m+2)x+2m+4,
即x2+(2m-2)x+2m+6=0,
方程至少有一个正根,有三种可能:
①有两个正根,此时可得
|
|
∴-3<m≤-1,
②有一个正根,一个负根,此时可得f(0)<0,得m<-3,
③有一个正根,另一根为零,此时可得
|
即
|
综合上述三种情况的m≤-1.
点评:本题考查的知识点是二次函数的性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
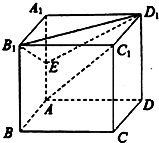 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,