题目内容
【题目】设![]() 是各项均为非零实数的数列
是各项均为非零实数的数列![]() 的前n项和,给出如下两个命题上:命题p:
的前n项和,给出如下两个命题上:命题p:![]() 是等差数列;命题q:等式
是等差数列;命题q:等式![]() 对任意
对任意![]()
![]() 恒成立,其中k,b是常数.
恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n![]() 和正数M,数列
和正数M,数列![]() 满足条件
满足条件![]() ,试求
,试求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,(2)必要条件,理由见解析,(3)
,(2)必要条件,理由见解析,(3)![]()
【解析】
(1)当![]() 是等差数列时,利用裂项求和的方法求得等式
是等差数列时,利用裂项求和的方法求得等式![]() 左边表达式的和,化简得
左边表达式的和,化简得![]() 对于
对于![]() 恒成立,由此求得
恒成立,由此求得![]() .
.
(2)当![]() 时,等式为
时,等式为![]()
![]() .利用退
.利用退![]() 作差法,证得数列
作差法,证得数列![]() 为等差数列,由此证得
为等差数列,由此证得![]() 是
是![]() 的必要条件.
的必要条件.
(3)利用三角换元的方法,将![]() 表示三角函数的形式,结合柯西不等式和不等式的性质,求得
表示三角函数的形式,结合柯西不等式和不等式的性质,求得![]() 的最大值.
的最大值.
(1)设![]() 的公差为d,则原等式可化为
的公差为d,则原等式可化为
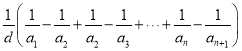
![]() ,
,
所以![]() ,
,
即![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() ,
,![]() .
.
(2)当![]() ,
,![]() 时,假设p是q的必要条件,即
时,假设p是q的必要条件,即
“若![]()
![]() ①对于任意的
①对于任意的![]() 恒成立,则
恒成立,则![]() 为等差数列”.
为等差数列”.
当![]() 时,
时,![]() 显然成立.
显然成立.
当![]() 时,若
时,若![]()
![]() ②,
②,
由①﹣②得,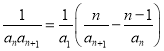 ,
,
即![]() ③.
③.
当![]() 时,
时,![]() ,即
,即![]() 、
、![]() 、
、![]() 成等差数列,
成等差数列,
当![]() 时,
时,![]() ④,
④,
即![]() .所以
.所以![]() 为等差数列,即p是q的必要条件.
为等差数列,即p是q的必要条件.
(3)由![]() ,可设
,可设![]()
![]() ,所以
,所以![]() .
.
设![]() 的公差为d,则
的公差为d,则![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
![]()
![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
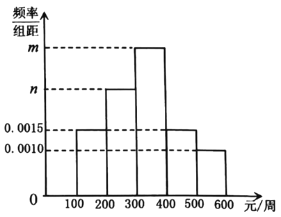
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()

