Question

【题目】已知椭圆 =1（a＞b＞0）右顶点与右焦点的距离为 ﹣1，短轴长为2 ． （Ⅰ）求椭圆的方程；
（Ⅱ）过左焦点F的直线与椭圆分别交于A、B两点，若△OAB（O为直角坐标原点）的面积为 ，求直线AB的方程．

Answer 1

【答案】解：（Ⅰ）∵椭圆 =1（a＞b＞0）右顶点与右焦点的距离为 ﹣1，短轴长为2 ．∴由题意得 ，
解得a= ，c=1
所以所求椭圆方程为 ．
（Ⅱ）当直线AB与x轴垂直时，|AB|= ，
此时S△AOB= 不符合题意故舍掉．
当直线AB与x轴不垂直时，设直线AB的方程为y=k（x+1），
由
消去y得：（2+3k2）x2+6k2x+（3k2﹣6）=0，
设A（x1 ， y1），B（x2 ， y2），则 ，
∴|AB|= =
= = =
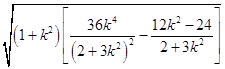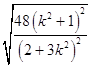原点O到直线的AB距离d= ，
∴三角形的面积 = = ，
解得k= ．
直线AB的方程为y= （x+1），或y=﹣ （x+1）．
即 ，或
【解析】（Ⅰ）由椭圆右顶点与右焦点的距离为 ﹣1，短轴长为2 ，列出方程组求出a，b，由此能求出椭圆方程．（Ⅱ）当直线AB与x轴垂直时，不符合题意；当直线AB与x轴不垂直时，设直线AB的方程为y=k（x+1），由 ，得：（2+3k2）x2+6k2x+（3k2﹣6）=0，由此利用韦达定理、弦长公式、点到直线的距离公式、三角形的面积公式，结合已知条件能求出直线AB的方程．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：，焦点在y轴：即可以解答此题．