题目内容
已知椭圆C: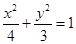 ,过点
,过点 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线 交椭圆
交椭圆 于
于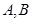 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 ,
,
(1)求证:直线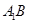 过
过 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(2)求: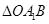 面积的取值范围。
面积的取值范围。
【答案】
(I)不妨设直线方程为 ,与
,与 联立并消去
联立并消去 得:
得:
 ,设
,设 ,则有
,则有 ,
, ,由
,由 关于
关于 轴的对称点为
轴的对称点为 ,得
,得 ,根据题意设直线
,根据题意设直线 与x轴相交于点
与x轴相交于点 ,
,
得 ,即
,即 ,整理得
,整理得 ,
,
 ,代入得
,代入得 ,则定点为
,则定点为
(II)由(I)中判别式 ,解得
,解得 ,而直线
,而直线 过定点
过定点
所以
记 ,
, ,易得
,易得 在
在 上位单调递减函数,得
上位单调递减函数,得 
【解析】略

练习册系列答案
相关题目
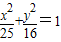 ,过点(3,0)的且斜率为
,过点(3,0)的且斜率为 的直线被C所截线段的中点坐标为( )
的直线被C所截线段的中点坐标为( )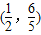
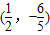
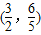
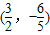
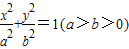 ,过点(-
,过点(-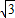 ,
, )离心率e=
)离心率e=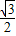 .
.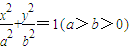 ,过点B(0,1),离心率为
,过点B(0,1),离心率为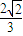 .
. 成立?若存在,求出直线l的方程;若不存在,请说明理由.
成立?若存在,求出直线l的方程;若不存在,请说明理由. ,过点P(4,0)且不与坐标轴垂直的直线l交椭圆C于A,B两点,设点A关于x轴的对称点为A1
,过点P(4,0)且不与坐标轴垂直的直线l交椭圆C于A,B两点,设点A关于x轴的对称点为A1