题目内容
设F1、F2为曲线C1:
+
=1的焦点,P是曲线C2:
-y2=1与C1的一个交点,则
的值为
.
| x2 |
| 6 |
| y2 |
| 2 |
| x2 |
| 3 |
| ||||
|
|
| 1 |
| 3 |
| 1 |
| 3 |
分析:先计算两曲线的焦点坐标,发现它们共焦点,再利用椭圆与双曲线定义,计算焦半径|PF1|,|PF2|,最后在焦点三角形PF1F2中,计算∠F1PF2=
即可
| ||||
|
|
解答:解:依题意,曲线C1:
+
=1的焦点为F1(-2,0),F2(2,0)
双曲线C2:
-y2=1的焦点也为F1(-2,0),F2(2,0)
∵P是曲线C2与C1的一个交点,设其为第一象限的点
由椭圆与双曲线定义可知
PF1+PF2=2
,PF1-PF2=2
解得PF1=
+
,PF2=
-
设∠F1PF2=θ
则cosθ=
=
=
故答案为:
| x2 |
| 6 |
| y2 |
| 2 |
双曲线C2:
| x2 |
| 3 |
∵P是曲线C2与C1的一个交点,设其为第一象限的点
由椭圆与双曲线定义可知
PF1+PF2=2
| 6 |
| 3 |
解得PF1=
| 6 |
| 3 |
| 6 |
| 3 |
设∠F1PF2=θ
则cosθ=
(
| ||||||||
2(
|
| 1 |
| 3 |
| ||||
|
|
故答案为:
| 1 |
| 3 |
点评:本题综合考查了椭圆与双曲线的定义,有一定的思维难度,用向量工具表达角的余弦值有一定的隐蔽性,解题时要透过现象看本质,用联系的观点解题

练习册系列答案
相关题目
 的值为
的值为 的焦点,P是曲线
的焦点,P是曲线 :
: 与C1的一个交点,
与C1的一个交点,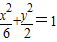 的焦点,P是曲线C2:
的焦点,P是曲线C2: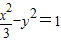 与C1的一个交点,则
与C1的一个交点,则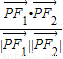 的值为( )
的值为( )



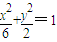 的焦点,P是曲线C2:
的焦点,P是曲线C2: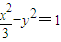 与C1的一个交点,则
与C1的一个交点,则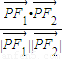 的值为( )
的值为( )



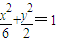 的焦点,P是曲线C2:
的焦点,P是曲线C2: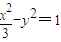 与C1的一个交点,则
与C1的一个交点,则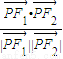 的值为( )
的值为( )


