题目内容
已知点P(0,b)是y轴上的动点,点F(1,0)、M(a,0)满足PM⊥PF,动点N满足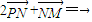 .
.(1)求动点N所在曲线C的方程.
(2)若曲线C上的两点A、B满足OA⊥OB(O为坐标原点,A、B不同于O点),试证明直线AB必过定点,并求出这个定点的坐标.
【答案】分析:(1)设动点N(x,y).依据题意,有 ,
, .由
.由 ,知
,知 ,由此能求出曲线C的方程.
,由此能求出曲线C的方程.
(2)因A、B是曲线C:y2=4x(x≥0)上不同于原点的两点,设 、
、 ,
,
则 、
、 ,
, .由OA⊥OB,知y1y2=-16.由直线AB的法向量为
.由OA⊥OB,知y1y2=-16.由直线AB的法向量为 ,得直线AB的方程:
,得直线AB的方程: ,由此能够证明直线AB:
,由此能够证明直线AB: 恒过定点,且定点坐标为(4,0).
恒过定点,且定点坐标为(4,0).
解答: 解:(1)设动点N(x,y). (1分)
解:(1)设动点N(x,y). (1分)
依据题意,有 ,
, .(3分)
.(3分)
又 ,
,
则 ,
,
进一步有 .
.
因此,y2=4x(x≥0). (7分)
所以曲线C的方程是y2=4x(x≥0). (8分)
(2)证明:因A、B是曲线C:y2=4x(x≥0)上不同于原点的两点,
可设 、
、 ,
,
则 、
、 ,
,
 . (11分)
. (11分)
又OA⊥OB,
故 .
.
所以y1y2=-16. (14分)
由直线AB的法向量为 ,
,
可得直线AB的方程: ,
,
进一步化简为 .(16分)
.(16分)
所以直线AB: 恒过定点,
恒过定点,
且定点坐标为(4,0). (18分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,
, .由
.由 ,知
,知 ,由此能求出曲线C的方程.
,由此能求出曲线C的方程.(2)因A、B是曲线C:y2=4x(x≥0)上不同于原点的两点,设
 、
、 ,
,则
 、
、 ,
, .由OA⊥OB,知y1y2=-16.由直线AB的法向量为
.由OA⊥OB,知y1y2=-16.由直线AB的法向量为 ,得直线AB的方程:
,得直线AB的方程: ,由此能够证明直线AB:
,由此能够证明直线AB: 恒过定点,且定点坐标为(4,0).
恒过定点,且定点坐标为(4,0).解答:
 解:(1)设动点N(x,y). (1分)
解:(1)设动点N(x,y). (1分)依据题意,有
 ,
, .(3分)
.(3分)又
 ,
,则
 ,
,进一步有
 .
.因此,y2=4x(x≥0). (7分)
所以曲线C的方程是y2=4x(x≥0). (8分)
(2)证明:因A、B是曲线C:y2=4x(x≥0)上不同于原点的两点,
可设
 、
、 ,
,则
 、
、 ,
, . (11分)
. (11分)又OA⊥OB,
故
 .
.所以y1y2=-16. (14分)
由直线AB的法向量为
 ,
,可得直线AB的方程:
 ,
,进一步化简为
 .(16分)
.(16分)所以直线AB:
 恒过定点,
恒过定点,且定点坐标为(4,0). (18分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
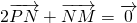 .
.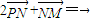 .
.