题目内容
如图，设抛物线C：x2＝4y的焦点为F，P(x0，y0)为抛物线上的任一点(其中x0≠0)，过P点的切线交y轴于Q点．
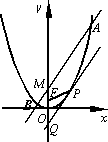
(1)证明：｜FP｜＝｜FQ｜；
(2)Q点关于原点O的对称点为M，过M点作平行于PQ的直线交抛物线C于A、B两点，若
(λ＞1)，求λ的值．
答案：
解析：
解析：
|
(1)证明：由抛物线定义知 得Q点坐标为(0，－y0)，∴ ∴|PF|＝|QF|，∴△PFQ为等腰三角形．(6分) (2)设A(x1，y1)，B(x2，y2)，又M点坐标为(0，y0)，∴AB方程为 由 由 ∴ 由①②知 ∴ |
，(2分)
，可得PQ所在直线方程为x0x＝2(y＋y0)，(4分)
，
，
得
①
得：
，
②
，得
，由x0≠0可得x2≠0，
，又
，解得：
．(12分)
练习册系列答案
相关题目
如图，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点．则△APB的重心G的轨迹方程为
如图，设抛物线C的方程为y2=4x，O为坐标原点，P为抛物线的准线与其对称轴的交点，过焦点F且垂直于x轴的直线交抛物线于M、N两点，若直线PM与ON相交于点Q，则cos∠MQN=