题目内容
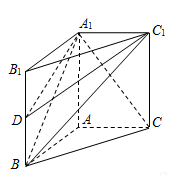
如图,在直三棱柱ABC—A1B1C1,AB=AC=1,∠BAC=90°,连结A1B与∠A1BC=60°.

(Ⅰ)求证:AC⊥A1B;
(Ⅱ)设D是BB1的中点,求三棱锥D-A1BC1的体积.
【答案】
(Ⅰ)详见解析;(Ⅱ)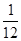
【解析】
试题分析:(Ⅰ)借助直三棱柱的性质和线面垂直的性质定理证明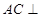 平面
平面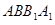 ,然后利用线面垂直的性质证明;(Ⅱ)证明
,然后利用线面垂直的性质证明;(Ⅱ)证明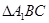 是正三角形,由
是正三角形,由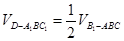 求解.
求解.
试题解析:(Ⅰ) 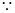 三棱柱
三棱柱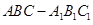 是直三棱柱,
是直三棱柱,
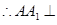 平面
平面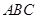 ,
,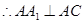 .
.
又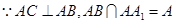 ,
,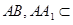 平面
平面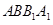
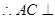 平面
平面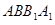 ,
,
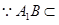 平面
平面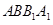 ,从而
,从而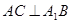 . (4分)
. (4分)
(Ⅱ)连结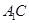 ,设
,设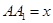 ,
,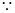
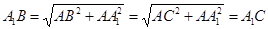 ,
,
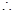
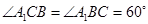 ,从而
,从而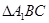 是正三角形,
是正三角形,
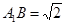 ,
,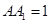 ,
(8分)
,
(8分)
又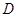 为
为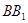 的中点.
的中点.
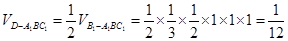 . (12分)
. (12分)
考点:三棱柱的性质,空间中的线线、线面垂直,三棱锥的体积.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目




