题目内容
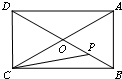 如图,矩形ABCD两条对角线相交于点O,∠BOC=120°,AB=3cm,一动点P以1cm/s的速度沿折线OB-BA运动,则点C,O,P围成的三角形的面积y与点P的运动时间x(s)
如图,矩形ABCD两条对角线相交于点O,∠BOC=120°,AB=3cm,一动点P以1cm/s的速度沿折线OB-BA运动,则点C,O,P围成的三角形的面积y与点P的运动时间x(s)之间的函数图象为( )
分析:先由题意表示出三角形的面积表达式,根据函数表达式可判断答案.
解答:解:∵∠BOC=120°,∴∠AOB=60°,
又AB=3cm,∴OB=OC=AB=3cm,
则BC2=OC2+OB2-2OC•OB•cos120°=9+9-2×3×3cos120°=27,
∴BC=3
,
当点P由点O到点B时,即0≤x≤3时,点C,O,P围成的三角形的面积:y=
×OC×OPsin∠BOC=
×3×x×sin120°=
x,
由选项可知选项C符合,
故选C.
又AB=3cm,∴OB=OC=AB=3cm,
则BC2=OC2+OB2-2OC•OB•cos120°=9+9-2×3×3cos120°=27,
∴BC=3
| 3 |
当点P由点O到点B时,即0≤x≤3时,点C,O,P围成的三角形的面积:y=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
由选项可知选项C符合,
故选C.
点评:本题考查函数在实际问题中的应用及函数图象,属基础题,由实际问题准确建立函数模型是解题关键.

练习册系列答案
相关题目
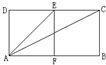 如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为
如图,矩形ABCD由两个正方形拼成,则∠CAE的正切值为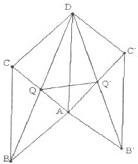 如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b. 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上. 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.