题目内容
设x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点,
(Ⅰ)若x1=-1,x2=2,求函数f(x)的解析式;
(Ⅱ)若|x1|+|x2|=2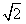 ,求b的最大值;
,求b的最大值;
(Ⅲ)设函数g(x)=f′(x)-a(x-x1),x∈(x1,x2),当x2=a时,求|g(x)|的最大值。
(Ⅰ)若x1=-1,x2=2,求函数f(x)的解析式;
(Ⅱ)若|x1|+|x2|=2
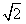 ,求b的最大值;
,求b的最大值;(Ⅲ)设函数g(x)=f′(x)-a(x-x1),x∈(x1,x2),当x2=a时,求|g(x)|的最大值。
解:(1)∵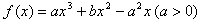 ,
,
∴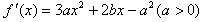 ,
,
依题意有-1和2是方程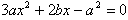 的两根,
的两根,
∴ ,
,
∴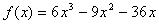 ,(经检验,适合)
,(经检验,适合)
(2)∵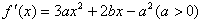 ,
,
依题意,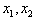 是方程f′(x)=0的两个根,
是方程f′(x)=0的两个根,
∵ ,
,
∴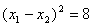 ,
,
∴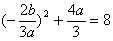 ,
,
∴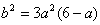 ,
,
∵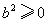 ,
,
∴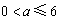 ,
,
设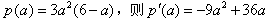 ,
,
由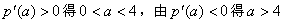 ,
,
即:函数p(a)在区间(0,4]上是增函数,在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为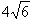 。
。
(3)证明:∵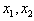 是方程f′(x)=0的两根,
是方程f′(x)=0的两根,
∴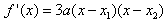 ,
,
∵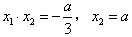 ,
,
∴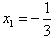 ,
,
∴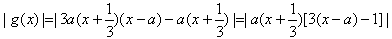 ,
,
∵ ,
,
∴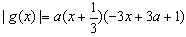 ,
,
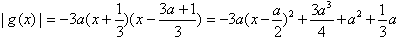
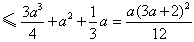 ,
,
∴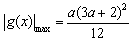 ,当且仅当
,当且仅当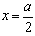 时取等号。
时取等号。
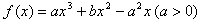 ,
,∴
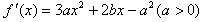 ,
,依题意有-1和2是方程
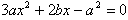 的两根,
的两根,∴
 ,
,∴
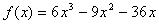 ,(经检验,适合)
,(经检验,适合) (2)∵
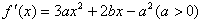 ,
,依题意,
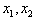 是方程f′(x)=0的两个根,
是方程f′(x)=0的两个根,∵
 ,
,∴
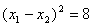 ,
,∴
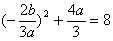 ,
,∴
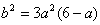 ,
, ∵
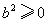 ,
,∴
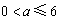 ,
,设
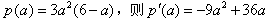 ,
,由
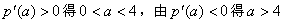 ,
,即:函数p(a)在区间(0,4]上是增函数,在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为
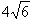 。
。(3)证明:∵
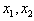 是方程f′(x)=0的两根,
是方程f′(x)=0的两根,∴
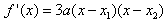 ,
,∵
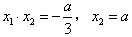 ,
,∴
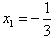 ,
,∴
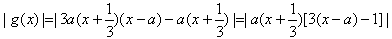 ,
,∵
 ,
,∴
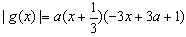 ,
,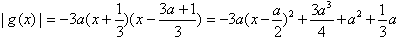
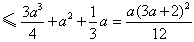 ,
,∴
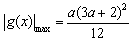 ,当且仅当
,当且仅当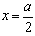 时取等号。
时取等号。
练习册系列答案
相关题目