题目内容
已知lg2=a，lg3=b，则lg36=
- A.2a+2b
- B.4ab
- C.2a+3b
- D.a2+b2
A
分析：直接把lg36用对数式的运算性质展开，化为仅含lg2和lg3的式子，代入lg2=a，lg3=b后答案可求．
解答：lg36=lg62=2lg6=2lg（2×3）=2lg2+2lg3．
∵lg2=a，lg3=b，
∴lg36=2lg2+2lg3=2a+2b．
故选A．
点评：本题考查了对数的运算性质，是基础的会考题型．
分析：直接把lg36用对数式的运算性质展开，化为仅含lg2和lg3的式子，代入lg2=a，lg3=b后答案可求．
解答：lg36=lg62=2lg6=2lg（2×3）=2lg2+2lg3．
∵lg2=a，lg3=b，
∴lg36=2lg2+2lg3=2a+2b．
故选A．
点评：本题考查了对数的运算性质，是基础的会考题型．
练习册系列答案
相关题目
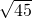的值为________．
的值为 ________．
；
的值为 ．