题目内容
素材1:三棱锥S—ABC的三个侧面和底面都成60°的二面角.素材2:∠BAC=60°且SA⊥BC，BA=6.
试根据上述素材构建一个问题然后再解答.
构建问题:三棱锥S—ABC的三个侧面与底面都成60°的角，并且∠BAC=60°，SA⊥BC，BA=6，求三棱锥S—ABC的表面积及体积.
解析：作SO⊥底面ABC于O，连结AO并延长交BC于D，连结SD.
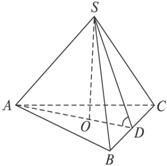
由题设可知O是△ABC的内心.
∴AD平分∠BAC.
∵SA⊥BC,SO⊥BC, ∴BC⊥AD.
又∠BAC=60°,则△ABC是等边三角形.
∴OD=
AD=
AB=
.
又BC⊥SD，∴SA=SB=SC.
由题设可知∠SDA=60°.
∴SD=2
,SO=3.
则S侧=
×6×2
×3=18
.
∴S表=S底+S侧=
×62+18
=27
，
VS-ABC=
S底·SO=
·
×62×3=9
.
练习册系列答案
阅读快车系列答案
相关题目
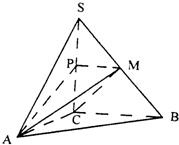如图，在三棱锥S-ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
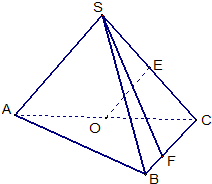如图，在三棱锥S-ABC中，侧面SAC与底面ABC垂直，E，O分别是SC、AC的中点，SA=SC=棱长均为1三棱锥S-ABC，若空间一点P满足
=x
+y
+z
(x+y+z=1)，则|
|的最小值为（ ）
| SP |
| SA |
| SB |
| SC |
| SP |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
，则
的最小值为
