题目内容
(本小题满分12分)
已知椭圆
 的离心率为
的离心率为 ,点
,点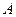 是椭圆上的一点,且点
是椭圆上的一点,且点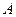 到椭圆
到椭圆 的两焦点的距离之和为4,
的两焦点的距离之和为4,
(1)求椭圆 的方程;
的方程;
(2)过点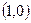 作直线
作直线 与椭圆
与椭圆 交于
交于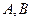 两点,
两点, 是坐标原点,设
是坐标原点,设 ,是否存在这样的直线
,是否存在这样的直线 ,使四边形
,使四边形 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
已知椭圆

 的离心率为
的离心率为 ,点
,点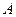 是椭圆上的一点,且点
是椭圆上的一点,且点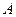 到椭圆
到椭圆 的两焦点的距离之和为4,
的两焦点的距离之和为4,(1)求椭圆
 的方程;
的方程;(2)过点
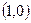 作直线
作直线 与椭圆
与椭圆 交于
交于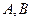 两点,
两点, 是坐标原点,设
是坐标原点,设 ,是否存在这样的直线
,是否存在这样的直线 ,使四边形
,使四边形 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。(1)

(2)不存在,证明略。
(1)
 …………….4分
…………….4分(2)
 ,所以四边形
,所以四边形 为平行四边形
为平行四边形假设存在直线
 ,使
,使
所以四边形
 为矩形,
为矩形,
设直线
 的斜率不存在,则直线的方程为
的斜率不存在,则直线的方程为
 则
则 所以
所以 舍
舍若直线的斜率存在,设直线的方程为

 故
故

 所以
所以 不存在
不存在综上,满足条件的直线不存在。………………12分

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 的顶点
的顶点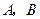 在椭圆
在椭圆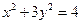 上,
上, 在直线
在直线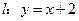 上,且
上,且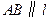 .
.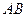 边通过坐标原点
边通过坐标原点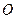 时,求
时,求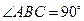 ,且斜边
,且斜边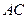 的长最大时,求
的长最大时,求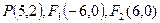
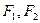 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;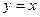 的对称点分别为
的对称点分别为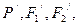 ,求以
,求以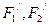 为焦点且过点
为焦点且过点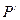 的双曲线的标准方程。
的双曲线的标准方程。 是椭圆
是椭圆 上的点,
上的点,  、
、 是椭圆的两个焦点,则
是椭圆的两个焦点,则 的值为( )
的值为( ) +
+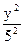 =1的焦点坐标为(0,4)和(0,—4).
=1的焦点坐标为(0,4)和(0,—4).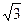 =0垂直的直线方程是2x + y-3=0.
=0垂直的直线方程是2x + y-3=0.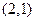 的距离与到定直线
的距离与到定直线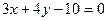 距离相等的点的轨迹是抛物线.
距离相等的点的轨迹是抛物线. 与椭圆
与椭圆 相交于不同的两点A、B,则使
相交于不同的两点A、B,则使 为整数的直线
为整数的直线 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为______________
轴上,长轴长是短轴长的两倍,则m的值为______________ 分别为具有公共焦点
分别为具有公共焦点 的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足 的值为
的值为 


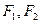 是椭圆
是椭圆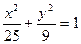 的两个焦点,过
的两个焦点,过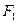 作直线与椭圆交于A,B两点,
作直线与椭圆交于A,B两点,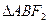 的周长为
的周长为