题目内容
(13分)如图,在三棱柱![]() 中,
中, ![]() ,
,
![]() ,
,![]() ,点D是
,点D是![]() 上一点,且
上一点,且![]() 。
。
 (1)求证:平面
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值。
的余弦值。
(13分)如图,在三棱柱![]() 中,
中, ![]() ,
,
![]() ,
,![]() ,点D是
,点D是![]() 上一点,且
上一点,且![]() .
.
 (1)求证:平面
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]()
(3)求二面角![]() 的余弦值.
的余弦值.
证明:(1)依题意,![]()
![]()
![]() ,
,
又![]() ,
,![]()
![]() ,又
,又![]()
![]() 平面
平面![]() 平面
平面![]() 4分
4分
(2)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 是
是![]() 的中点,连结
的中点,连结![]() .
.
由(Ⅰ)知![]() ,
,![]() ,
,![]() 是
是![]() 中点
中点
![]()
又![]() ,
,![]()
![]() 平面
平面![]() . 8分
. 8分
(3)如图,建立空间直角坐标系![]() ,设
,设![]() ,
,
 则
则![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]()
即![]() ,令
,令![]() ,
,![]() .
.
取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则cos![]() .
.
所以二面角![]() 大小的余弦值为
大小的余弦值为![]() . 13分
. 13分

练习册系列答案
相关题目
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,
如图,在三棱柱中,已知AB⊥侧面BB1C1C,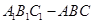 中,
中,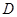 ,
,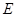 ,
,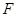 分别为
分别为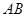 ,
, ,
,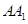 的中点,设三棱锥
的中点,设三棱锥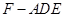 体积为
体积为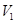 ,三棱柱
,三棱柱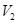 ,则
,则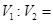

 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则 与平面
与平面 所成的角是
所成的角是
 B.
B. C.
C.  D.
D.
 中,
中, 侧面
侧面 ,且
,且 与底面成
与底面成 角,
角, ,则该棱柱体积的 最小值为
.
,则该棱柱体积的 最小值为
. 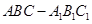 中,
中,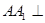 面
面 ,
,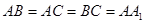 ,
, ,
, 分别为
分别为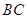 ,
,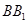 的中点.
的中点.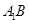 ∥平面
∥平面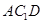 ; (2)求证:
; (2)求证: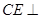 平面
平面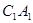 与平面
与平面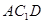 所成的角的正弦值.
所成的角的正弦值.