题目内容
已知函数 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
【答案】
D
【解析】
试题分析:因为函数 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,所以函数在
,所以函数在 时是减函数,而t=
时是减函数,而t= 在
在 时 是减函数,所以a>1,且
时 是减函数,所以a>1,且 时,
时, =
= ,解得
,解得 ,故实数
,故实数 的取值范围是
的取值范围是 ,选D。
,选D。
考点:本题主要考查复合函数、对数函数的单调性。
点评:小综合题,复合函数的单调性判断依据:内外层函数“同增异减”。对于对数函数,要注意真数大于零。

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
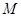 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意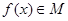 ,
,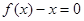 有实数根;② 函数
有实数根;② 函数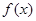 的导数
的导数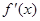 满足
满足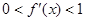 .
.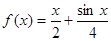 是否是集合
是否是集合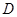 ,则对于任意
,则对于任意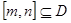 ,都存在
,都存在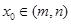 ,使得等式
,使得等式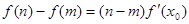 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程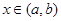 ,求证:对于
,求证:对于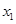 ,
,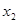 ,
,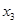 ,当
,当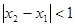 ,且
,且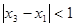 时,
时,
 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.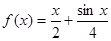 是否是集合
是否是集合 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 ,求证:对于
,求证:对于 ,
, ,
,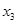 ,当
,当 ,且
,且 时,
时, .
.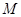 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意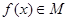 ,①方程
,①方程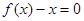 有实数根;②函数
有实数根;②函数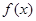 的导数
的导数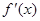 满足
满足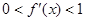 .
.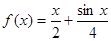 是否是集合
是否是集合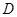 ,则对于任意
,则对于任意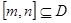 ,都存在
,都存在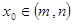 ,使得等式
,使得等式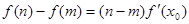 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程