题目内容
已知函数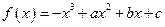 在
在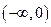 上是减函数,在
上是减函数,在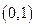 上是增函数,函数
上是增函数,函数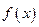 在
在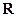 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求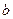 的值;
的值;
(2)求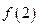 的取值范围;
的取值范围;
(3)试探究直线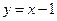 与函数
与函数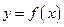 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
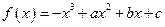 在
在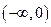 上是减函数,在
上是减函数,在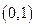 上是增函数,函数
上是增函数,函数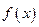 在
在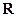 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.(1)求
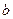 的值;
的值;(2)求
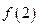 的取值范围;
的取值范围;(3)试探究直线
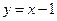 与函数
与函数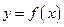 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.(1)0(2)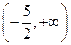 (3)见解析
(3)见解析
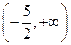 (3)见解析
(3)见解析(1)解:∵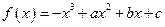 ,∴
,∴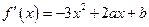 .
.
∵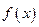 在
在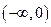 上是减函数,在
上是减函数,在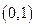 上是增函数,
上是增函数,
∴当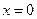 时,
时,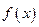 取到极小值,即
取到极小值,即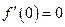 .
.
∴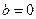 .
.
(2)解:由(1)知,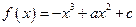 ,
,
∵1是函数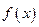 的一个零点,即
的一个零点,即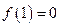 ,∴
,∴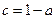 .
.
∵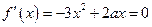 的两个根分别为
的两个根分别为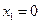 ,
,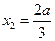 .
.
∵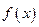 在
在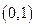 上是增函数,且函数
上是增函数,且函数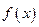 在
在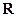 上有三个零点,
上有三个零点,
∴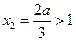 ,即
,即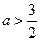 .∴
.∴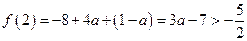 .
.
故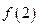 的取值范围为
的取值范围为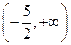 .
.
(3)解:由(2)知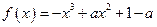 ,且
,且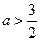 .
.
要讨论直线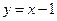 与函数
与函数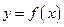 图像的交点个数情况,
图像的交点个数情况,
即求方程组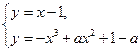 解的个数情况.
解的个数情况.
由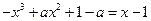 ,得
,得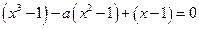 .
.
即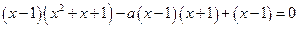 .
.
即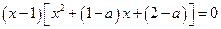 .
.
∴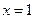 或
或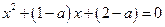 .
.
由方程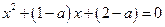 , (*)
, (*)
得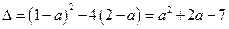 .
.
∵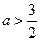 ,
,
若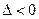 ,即
,即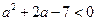 ,解得
,解得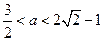 .此时方程(*)无实数解.
.此时方程(*)无实数解.
若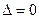 ,即
,即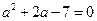 ,解得
,解得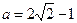 .此时方程(*)有一个实数解
.此时方程(*)有一个实数解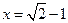 .
.
若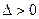 ,即
,即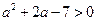 ,解得
,解得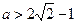 .此时方程(*)有两个实数解,分别为
.此时方程(*)有两个实数解,分别为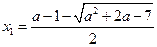 ,
,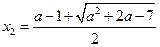 .
.
且当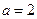 时,
时,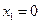 ,
,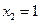 .
.
综上所述,当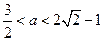 时,直线
时,直线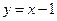 与函数
与函数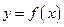 的图像有一个交点.
的图像有一个交点.
当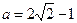 或
或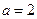 时,直线
时,直线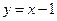 与函数
与函数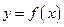 的图像有二个交点.
的图像有二个交点.
当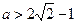 且
且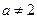 时,直线
时,直线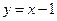 与函数
与函数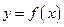 的图像有三个交点.
的图像有三个交点.
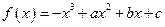 ,∴
,∴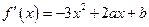 .
.∵
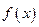 在
在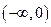 上是减函数,在
上是减函数,在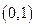 上是增函数,
上是增函数,∴当
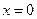 时,
时,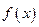 取到极小值,即
取到极小值,即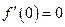 .
.∴
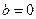 .
.(2)解:由(1)知,
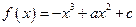 ,
,∵1是函数
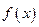 的一个零点,即
的一个零点,即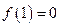 ,∴
,∴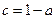 .
.∵
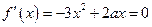 的两个根分别为
的两个根分别为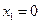 ,
,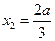 .
.∵
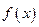 在
在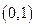 上是增函数,且函数
上是增函数,且函数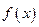 在
在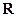 上有三个零点,
上有三个零点,∴
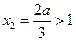 ,即
,即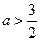 .∴
.∴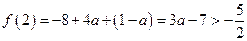 .
.故
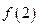 的取值范围为
的取值范围为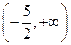 .
.(3)解:由(2)知
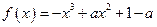 ,且
,且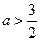 .
.要讨论直线
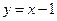 与函数
与函数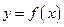 图像的交点个数情况,
图像的交点个数情况,即求方程组
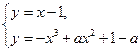 解的个数情况.
解的个数情况.由
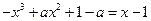 ,得
,得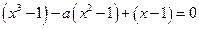 .
.即
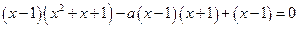 .
.即
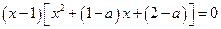 .
.∴
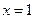 或
或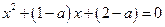 .
.由方程
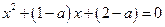 , (*)
, (*)得
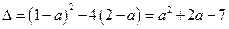 .
.∵
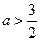 ,
,若
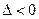 ,即
,即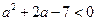 ,解得
,解得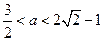 .此时方程(*)无实数解.
.此时方程(*)无实数解.若
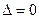 ,即
,即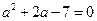 ,解得
,解得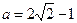 .此时方程(*)有一个实数解
.此时方程(*)有一个实数解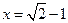 .
.若
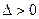 ,即
,即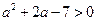 ,解得
,解得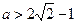 .此时方程(*)有两个实数解,分别为
.此时方程(*)有两个实数解,分别为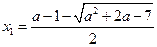 ,
,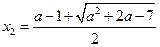 .
.且当
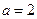 时,
时,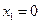 ,
,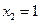 .
.综上所述,当
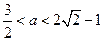 时,直线
时,直线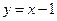 与函数
与函数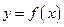 的图像有一个交点.
的图像有一个交点.当
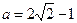 或
或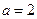 时,直线
时,直线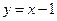 与函数
与函数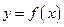 的图像有二个交点.
的图像有二个交点.当
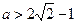 且
且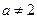 时,直线
时,直线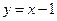 与函数
与函数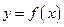 的图像有三个交点.
的图像有三个交点.
练习册系列答案
相关题目
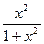

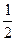 ),f(3)与f(
),f(3)与f(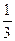 );
);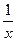 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;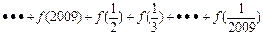 的值.
的值.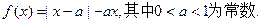
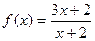 ,
,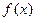 图象的对称中心;
图象的对称中心;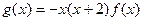 ,求
,求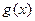 在区间
在区间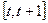 上的最大值
上的最大值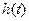 ;
;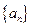 满足
满足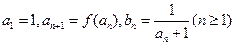 ,
,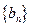 的通项公式
的通项公式
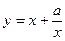 有如下性质:如果常数
有如下性质:如果常数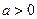 ,那么该函数在(0,
,那么该函数在(0,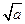 )上减函数,在
)上减函数,在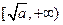 是增函数。
是增函数。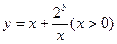 的值域为
的值域为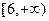 ,求
,求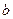 的值;
的值;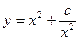 (常数
(常数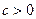 )在定义域的单调性,并说明理由;
)在定义域的单调性,并说明理由;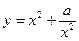 (常数
(常数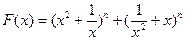 (n是正整数)在区间[
(n是正整数)在区间[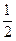 ,2]上的最大值和最小值(可利用你的研究结论)。
,2]上的最大值和最小值(可利用你的研究结论)。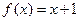 ,设
,设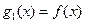 ,
,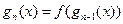
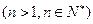
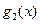 ,
,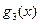 的表达式,并猜想
的表达式,并猜想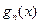
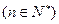 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)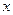 的函数
的函数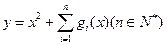 在区间
在区间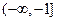 上的最小值为6,求
上的最小值为6,求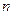 的值
的值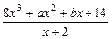 ,定义域为[-1,1]
,定义域为[-1,1]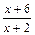 均成立,求实数a,b的值.
均成立,求实数a,b的值.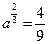 (a>0) ,则
(a>0) ,则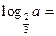 。
。