题目内容
已知函数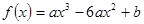 ,问是否存在实数
,问是否存在实数 使
使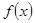 在
在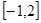 上取最大值3,最小值-29,若存在,求出
上取最大值3,最小值-29,若存在,求出 的值;不存在说明理由。
的值;不存在说明理由。
【答案】
(1) ;(2)
;(2)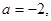
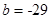 或
或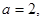
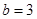
【解析】
试题分析:显然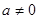 ,
,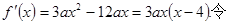
 解得
解得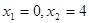 (舍去)
(舍去)
(1)当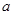 >0时,
>0时,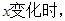
 的变化情况如下:
的变化情况如下:
|
|
|
0 |
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
所以当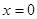 时,
时,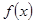 取得最大值,故
取得最大值,故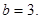
又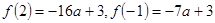 ,
,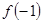 >
>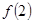
所以当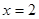 时,
时,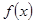 取得最小值,
取得最小值,
(2)当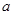 <0时,
<0时,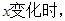
 的变化情况如下:
的变化情况如下:
|
|
|
0 |
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
所以当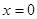 时,
时,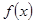 取得最小值,故
取得最小值,故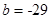
又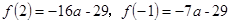 ,
, 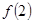 >
>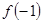
所以当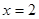 时,
时,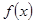 取得最大小值,
取得最大小值,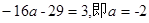
综上所述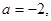
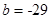 或
或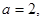
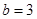
考点:本题主要考查导数计算,应用导数研究函数的单调性、最值,利用导数证明不等式。
点评:典型题,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。求最值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值、计算得到函数值比较大小。本题利用“本解法”,直观明了。

练习册系列答案
相关题目









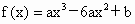 ,问是否存在实数a、b,使f(x)在[-1,2]上取得最大值3,最小值为-29,若存在,求出a、b的值;若不存在,请说明理由.
,问是否存在实数a、b,使f(x)在[-1,2]上取得最大值3,最小值为-29,若存在,求出a、b的值;若不存在,请说明理由.