题目内容
已知函数f(x)在定义域(-∞,1]上是减函数,问是否存在实数k,使不等式f(-
)≥f(k2-sin2x)对一切实数x恒成立?若成立,求出k的取值范围,若不成立,说明理由.
| 1 | 2 |
分析:先假设存在实数k满足题意,再函数的单调性和不等式,列出对应的不等式,注意自变量与定义域的关系,再由0≤sin2x≤1求出k的范围即可.
解答:解:假设存在实数k满足题意,
∵f(x)在定义域(-∞,1]上是减函数,
∴
,即-1+k2≤sin2x≤
+k2一切实数x恒成立,
∵0≤sin2x≤1,∴
,解得
≤k2≤1,
则-1≤k≤-
或
≤k≤1,
故当-1≤k≤-
或
≤k≤1时不等式恒成立.
∵f(x)在定义域(-∞,1]上是减函数,
∴
|
| 1 |
| 2 |
∵0≤sin2x≤1,∴
|
| 1 |
| 2 |
则-1≤k≤-
| ||
| 2 |
| ||
| 2 |
故当-1≤k≤-
| ||
| 2 |
| ||
| 2 |
点评:本题考查了函数的单调性,正弦函数的值域的应用,以及恒成立的转化问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
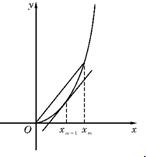 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.