题目内容
已知函数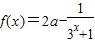 (a∈R).
(a∈R).(1)若函数f(x)为奇函数,求a的值;
(2)判断函数f(x)在R上的单调性,并证明.
【答案】分析:(1)直接根据函数f(x)为奇函数,对应的f(-x)+f(x)=0恒成立即可求出a的值;
(2)直接根据对数函数的单调性以及对数的值域按单调性的证明过程即可得到结论.
解答:解:(1)∵函数f(x)为奇函数,
∴f(-x)+f(x)=0,
即: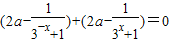 ,
,
则有: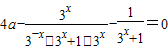 ,
,
即: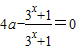 ,
,
∴4a-1=0,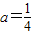 ;
;
(2)f(x)在R上是增函数,证明如下:
任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=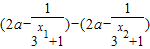 =
=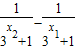 =
=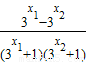 .
.
∵y=3x在R上是增函数,且x1<x2,
∴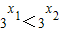 ,
,
即: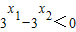 .
.
又3x>0,
∴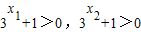 ,
,
∴f(x1)-f(x2)<0,
即:f(x1)<f(x2),
故f(x)在R上是增函数.
点评:本题主要考察函数奇偶性与单调性的综合.解决问题的关键在于把问题转化为f(-x)+f(x)=0恒成立求出a的值.
(2)直接根据对数函数的单调性以及对数的值域按单调性的证明过程即可得到结论.
解答:解:(1)∵函数f(x)为奇函数,
∴f(-x)+f(x)=0,
即:
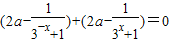 ,
,则有:
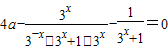 ,
,即:
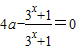 ,
,∴4a-1=0,
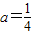 ;
;(2)f(x)在R上是增函数,证明如下:
任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=
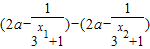 =
=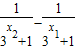 =
=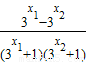 .
.∵y=3x在R上是增函数,且x1<x2,
∴
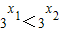 ,
,即:
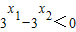 .
.又3x>0,
∴
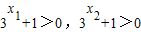 ,
,∴f(x1)-f(x2)<0,
即:f(x1)<f(x2),
故f(x)在R上是增函数.
点评:本题主要考察函数奇偶性与单调性的综合.解决问题的关键在于把问题转化为f(-x)+f(x)=0恒成立求出a的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).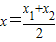 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.