题目内容
已知O是△ABC内一点，且满足
•
=
•
=
•
，则O点一定是△ABC的（ ）
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
分析：利用
•
=
•
=
•
，由平面向量的运算法则，能推导出
⊥
，
⊥
，
⊥
，由此能求出结果．
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
| OB |
| CA |
| OA |
| CB |
| OC |
| AB |
解答：解：O是△ABC内一点，且满足
•
=
•
=
•
，
∴
•
-
•
=0，
∴
•(
-
)=
•
=0，
∴
⊥
，
∵
•
-
•
=0，
∴
•(
-
)=
•
=0，
∴
⊥
，
∵
•
-
•
=0，
∴
•(
-
)=
•
=0，
∴
⊥
，
∴O点一定是△ABC的垂心．
故选C．
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
∴
| OA |
| OB |
| OB |
| OC |
∴
| OB |
| OA |
| OC |
| OB |
| CA |
∴
| OB |
| CA |
∵
| OA |
| OB |
| OC |
| OA |
∴
| OA |
| OB |
| OC |
| OA |
| CB |
∴
| OA |
| CB |
∵
| OB |
| OC |
| OC |
| OA |
∴
| OC |
| OB |
| OA |
| OC |
| AB |
∴
| OC |
| AB |
∴O点一定是△ABC的垂心．
故选C．
点评：本题考查平面向量的应用，解题时要注意平面运算法则的灵活运用，是基础题．
练习册系列答案
相关题目
已知O为平面内一定点，设条件p：动点M满足
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
，则∠AOB，∠BOC，∠COA
=
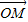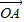+λ（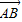
+
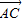），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）