题目内容
若偶函数f(x)在区间(-∞,-1]上是增函数,则( )
A.f(-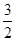 )<f(-1)<f(2) )<f(-1)<f(2) | B.f(-1)<f(-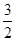 )<f(2) )<f(2) |
C.f(2)<f(-1)<f(-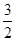 ) ) | D.f(2)<f(-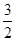 )<f(-1) )<f(-1) |
D
解析试题分析:由函数的奇偶性、单调性把f(2)、f(-1.5)、f(-1)转化到区间(-∞,-1]上进行比较即可解:因为f(x)在(-∞,-1]上是增函数,又-2<-1.5<-1≤-1,所以f(-2)<f(-1.5)<f(-1),又f(x)为偶函数,f(-2)=f(2),所以f(2)<f(-1.5)<f(-1).故选D
考点:函数的奇偶性
点评:本题考查函数的奇偶性、单调性的综合运用,解决本题的关键是灵活运用函数性质把f(2)、f(-1.5)、f(-1)转化到区间(-∞,-1]上解决.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
函数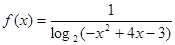 的定义域为( )
的定义域为( )
| A.(1,2)∪(2,3) | B.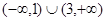 |
| C.(1,3) | D.[1,3] |
若函数 的导函数
的导函数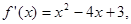 则函数
则函数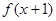 的单调递减区间是( )
的单调递减区间是( )
| A.(2,4) | B.(-3,-1) | C.(1,3) | D.(0,2) |
下列函数在其定义域内,既是奇函数又存在零点的是: ( )
A. | B.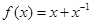 | C.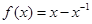 | D.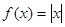 |
设f(x)为定义在R上的奇函数,当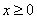 时,
时,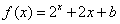 (
(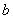 为常数),则
为常数),则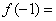 ( )
( )
| A.3 | B.1 | C.-1 | D.-3 |
函数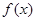 对任意自然数
对任意自然数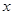 ,满足
,满足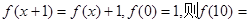 ( )
( )
| A.11 | B.12 | C.13 | D.14 |
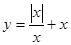 的图象是( )
的图象是( )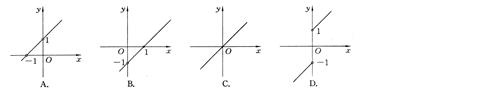
 在定义域内可导,
在定义域内可导,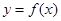 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数 的图象可能是( )
的图象可能是( )