题目内容
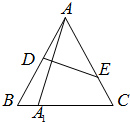 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0°,60°],用θ表示AD
(2)求AD长度的最小值.
解:(1)设A1B=x,AD=y,在△A1BD中,BD=1-y,A1D=AD=y,
由余弦定理可得y2=(1-y)2+x2-2x(1-y)cos60°
=(1-y)2+x2-x+xy,
∴x2-x+xy-2y+1=0,y=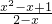 (0≤x≤1),
(0≤x≤1),
设∠A1AB=θ∈[0°,60°],
则在△A1BAz中,由正弦定理得,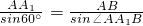 =
=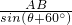 ,
,
∴AA1=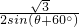
∴AD=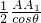 =
=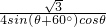 θ∈[0°,60°]
θ∈[0°,60°]
(2)y=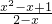 (0≤x≤1),
(0≤x≤1),
令t=2-x∈[1,2],∴y= =
=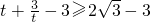
当且仅当t= 时,即x=2-
时,即x=2- 时等号成立,AD长度的最小值为2
时等号成立,AD长度的最小值为2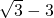 .
.
AD=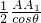 =
=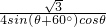
∵4sin(θ+60°)cosθ=2siθcosθ+2 cos2θ=sin2θ+
cos2θ=sin2θ+ (1+cos2θ)=2sin(2θ+60°)+
(1+cos2θ)=2sin(2θ+60°)+ .
.
因为θ∈[0°,60°]
所以2θ+60°∈[60°,180°]∴sin(2θ+60°)∈[0,1],
4sin(θ+60°)cosθ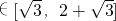 ,∴AD
,∴AD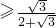 =
= (2-
(2- ),
),
∴AD长度的最小值为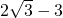 ,当且仅当
,当且仅当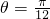 时取最小值.
时取最小值.
分析:(1)①设A1B=x,通过三角形直接表示AD,②设∠A1AB=θ∈[0°,60°],用余弦定理表示x与y的关系,利用正弦定理求出AA1,然后用θ表示AD.
(2)利用换元法以及基本不等式直接求出求AD长度的最小值.通过两角和的正弦函数化简AD的表达式,通过θ的范围求解三角函数的最值.
点评:本题考查解三角形的知识,余弦定理的应用,两角和的正弦函数,三角函数的最值的求法,基本不等式的应用,考查计算能力.
由余弦定理可得y2=(1-y)2+x2-2x(1-y)cos60°
=(1-y)2+x2-x+xy,
∴x2-x+xy-2y+1=0,y=
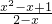 (0≤x≤1),
(0≤x≤1),设∠A1AB=θ∈[0°,60°],
则在△A1BAz中,由正弦定理得,
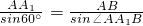 =
=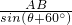 ,
,∴AA1=
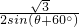
∴AD=
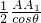 =
=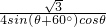 θ∈[0°,60°]
θ∈[0°,60°](2)y=
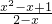 (0≤x≤1),
(0≤x≤1),令t=2-x∈[1,2],∴y=
 =
=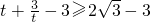
当且仅当t=
 时,即x=2-
时,即x=2- 时等号成立,AD长度的最小值为2
时等号成立,AD长度的最小值为2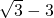 .
.AD=
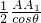 =
=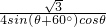
∵4sin(θ+60°)cosθ=2siθcosθ+2
 cos2θ=sin2θ+
cos2θ=sin2θ+ (1+cos2θ)=2sin(2θ+60°)+
(1+cos2θ)=2sin(2θ+60°)+ .
.因为θ∈[0°,60°]
所以2θ+60°∈[60°,180°]∴sin(2θ+60°)∈[0,1],
4sin(θ+60°)cosθ
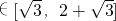 ,∴AD
,∴AD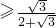 =
= (2-
(2- ),
),∴AD长度的最小值为
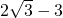 ,当且仅当
,当且仅当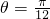 时取最小值.
时取最小值.分析:(1)①设A1B=x,通过三角形直接表示AD,②设∠A1AB=θ∈[0°,60°],用余弦定理表示x与y的关系,利用正弦定理求出AA1,然后用θ表示AD.
(2)利用换元法以及基本不等式直接求出求AD长度的最小值.通过两角和的正弦函数化简AD的表达式,通过θ的范围求解三角函数的最值.
点评:本题考查解三角形的知识,余弦定理的应用,两角和的正弦函数,三角函数的最值的求法,基本不等式的应用,考查计算能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
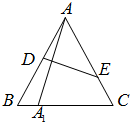 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
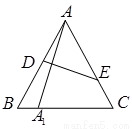
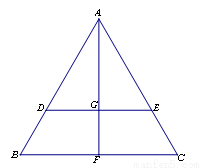
 中,
中, 分别是
分别是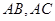 边上的点,
边上的点,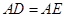 ,
,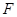 是
是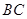 的中点,
的中点,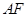 与
与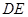 交于点
交于点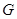 ,将
,将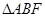 沿
沿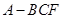 ,其中
,其中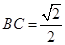 .
.
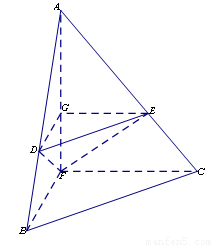
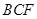 ;
;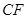
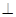 平面
平面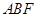 ;
;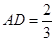 时,求三棱锥
时,求三棱锥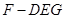 的体积
的体积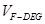 .
.