题目内容
抛物线y2=2px的焦点弦AB的中点为M,A、B、M在准线上的射影依次为C、D、N.求证:(1)A、O、D三点共线,B、O、C三点共线;
(2)FN⊥AB(F为抛物线的焦点).
证明:(1)设A(x1,y1)、B(x2,y2)、中点M(x0,y0),焦点F的坐标是(![]() ,0).
,0).
由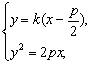 得ky2-2py-kp2=0.
得ky2-2py-kp2=0.
∴A、B、M在准线上的射影依次为C、D、N.
∴C(-![]() ,y1)、D(-
,y1)、D(-![]() ,y2)、N(-
,y2)、N(-![]() ,y0).
,y0).
∵kOA=![]() =
=![]() =
=![]() ,kOD=
,kOD=![]() ,
,
由ky2-2py-kp2=0,
得y1y2=![]() =-p2.
=-p2.
∴kOA=kOD.∴A、O、D三点共线.同理可证B、O、C三点共线.
(2)kFN=![]() ,当x1=x2时,显然FN⊥AB;当x1≠x2时,kAB=
,当x1=x2时,显然FN⊥AB;当x1≠x2时,kAB=![]() =
=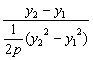 =
=![]() =
=![]() ,
,
∴kFN·kAB=-1.
∴FN⊥AB.综上所述知FN⊥AB成立.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
若抛物线y2=2px的焦点与双曲线
2-y2=1的右焦点重合,则p的值为( )
| x |
| 3 |
A、2
| ||
| B、4 | ||
| C、-4 | ||
| D、2 |