题目内容
已知数列
中，
，
，
是数列的前
项和，且
，
.
（1）求
的值；
（2）求数列的通项公式；
（3）若
是数列
的前项和，且
对一切都成立，求实数
取值范围.
【答案】
（Ⅰ）
（Ⅱ）
，
. （Ⅲ）
【解析】
，考查数列中
的关系，
，
裂项求和法，得
因为
对一切都成立，恒成立求实数
的取值范围时，一般分离参数，
再在最值处成立即可
解：（Ⅰ）因为，，所以 …….. 3分
（Ⅱ）由（Ⅰ）可知 
， 所以
所以所以
所以当
时，
所以
，，
，
，所以
所以，. 因为
满足上式，
所以，.
………….. 6分
（Ⅲ）当时，
…………….. 7分
又
， 所以
…………….. 9分
所以
………….. 10分
因为对一切都成立，
即
对一切都成立.
所以.
……………….. 12分
因为
，当且仅当
，即
时等号成立.
所以
. 所以
所以
练习册系列答案
相关题目
中，
，
，通项
是项数
的一次函数，
；
是由
组成，试归纳
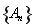
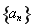
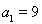
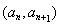
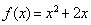
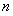
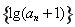
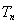
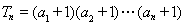
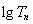
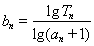
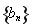
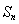
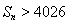
满足
，则称数列
中，
，点
在函数
的图像上，其中
为正整数。
是“平方递推数列”，且数列
为等比数列。
，即
，求数列
，求数列
的前
，并求使
的
中，
，
，通项
是项数
的一次函数，
；
是由
组成，试归纳
满足
,则称数列
中，
，点
在函数
的图象上，其中
为正整数．
是“平方递推数列”，且数列
为等比数列；
项积为
，即
，求
；
，求数列
的前
，并求使
的