题目内容
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(Ⅰ)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前 项积为
项积为 ,即
,即 ,求
,求 ;
;
(Ⅲ)在(Ⅱ)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和 ,并求使
,并求使 的
的 的最小值.
的最小值.
【答案】
(Ⅰ)见解析;(Ⅱ) ; (Ⅲ)
; (Ⅲ)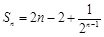 ,
,
【解析】
试题分析:(Ⅰ)将点的坐标代入函数解析式得 ,由定义可知
,由定义可知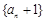 是“平方递推数列”. 由
是“平方递推数列”. 由 得
得 是以
是以 为首项,2为公比的等比数列;
为首项,2为公比的等比数列;
(Ⅱ)先由(Ⅰ)中等比数列得 ,故:
,故: ;
;
(Ⅲ)先求得 ,再求
,再求 ,由
,由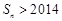 ,得
,得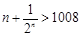 ,从而解得
,从而解得 .
.
试题解析:(I)由题意得: , 即
, 即  ,
,
则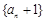 是“平方递推数列”.
2分
是“平方递推数列”.
2分
又有 得
得 是以
是以 为首项,2为公比的等比数列.4分
为首项,2为公比的等比数列.4分
(II)由(I)知 ,
5分
,
5分
 .8分
.8分
(III) ,
9分
,
9分
 ,
10分
,
10分
又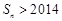 ,即
,即 ,
,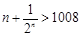 ,
,
又  ,
,
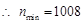 .
13分
.
13分
考点:1.等比数列的判定;2.数列求和;3.数列不等式的解法

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
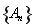

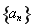
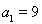
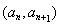
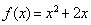
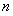

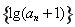
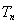
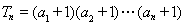
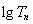
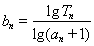
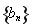
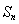
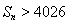
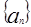 满足
满足 ,则称数列
,则称数列