题目内容
已知直线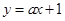 与双曲线
与双曲线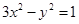 交于
交于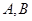 两点,
两点,
(1)若以 线段为直径的圆过坐标原点,求实数
线段为直径的圆过坐标原点,求实数 的值。
的值。
(2)是否存在这样的实数 ,使
,使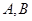 两点关于直线
两点关于直线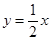 对称?说明理由.
对称?说明理由.
(1)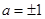 (2)不存在这样的a,使A(
(2)不存在这样的a,使A( ),B(
),B(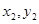 )关于直线
)关于直线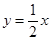 对称
对称
解析试题分析:(1)联立方程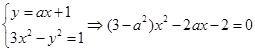 ,
,
设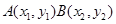 ,那么:
,那么: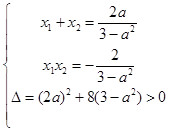
由于以AB线段为直径的圆经过原点,那么: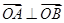 ,即
,即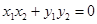 。
。
所以: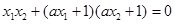 ,得到:
,得到: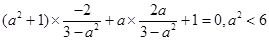 ,解得
,解得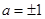 6分
6分
(2)假定存在这样的a,使A( ),B(
),B(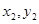 )关于直线
)关于直线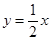 对称。
对称。
那么: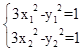 ,两式相减得:
,两式相减得: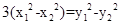 ,从而
,从而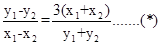
因为A( ),B(
),B(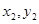 )关于直线
)关于直线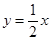 对称,所以
对称,所以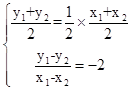
代入(*)式得到:-2=6,矛盾。
也就是说:不存在这样的a,使A( ),B(
),B(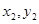 )关于直线
)关于直线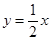 对称。 13分
对称。 13分
考点:直线与双曲线的位置关系
点评:第一问中首先将以AB为直径的圆经过原点转化为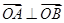 ,进而可用点的坐标表示,第二问中把握好对称的两个条件:A,B的中点在直线上,过A,B两点的直线与已知直线互相垂直
,进而可用点的坐标表示,第二问中把握好对称的两个条件:A,B的中点在直线上,过A,B两点的直线与已知直线互相垂直

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 平行且距离等于
平行且距离等于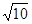 的直线方程。
的直线方程。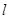 过点P(-2,1),
过点P(-2,1),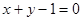 平行,求直线
平行,求直线 中,
中,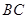 边上的高所在的直线的方程为
边上的高所在的直线的方程为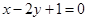 ,
, 的平分线所在直线的方程为
的平分线所在直线的方程为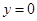 ,若点
,若点 的坐标为
的坐标为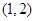 。
。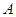 的坐标;
的坐标;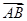 =(4,2).
=(4,2). 、
、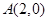 、
、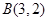 ,
,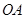 边上的中线所在直线为
边上的中线所在直线为 .(1)求
.(1)求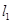 :
: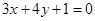 和点
和点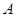 (1,2),设过
(1,2),设过 .
. 垂直,并且与原点的距离是5的直线的方程.
垂直,并且与原点的距离是5的直线的方程.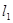 经过点
经过点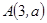 ,
,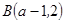 ,直线
,直线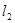 经过点
经过点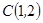 ,
,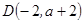 。
。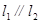 ,求
,求 的值。
的值。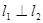 ,求
,求