题目内容
f(x)=kx+b,f(1)=0,f(3)=-
,求f(4)的值.
| 1 | 2 |
分析:由f(x)=kx+b,f(1)=0,f(3)=-
,推导出f(x)=-
x+
,由此能求出f(4).
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:∵f(x)=kx+b,f(1)=0,f(3)=-
,
∴
,
解得k=-
,b=
,
∴f(x)=-
x+
,
∴f(4)=-
×4+
=-
.
| 1 |
| 2 |
∴
|
解得k=-
| 1 |
| 4 |
| 1 |
| 4 |
∴f(x)=-
| 1 |
| 4 |
| 1 |
| 4 |
∴f(4)=-
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题考查一次函数的图象和性质的应用,解题时要认真审题,注意函数值的求法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
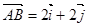 (
(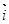 、
、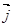 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.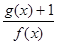 的最小值.
的最小值.