题目内容
已知α+2β=
,α和β为锐角;
(1)若tan(α+β)=2+
;求β;
(2)若tanβ=(2-
)cot
,满足条件的α和β是否存在?若存在,请求出α和β的值;若不存在,请说明理由.
| 2π |
| 3 |
(1)若tan(α+β)=2+
| 3 |
(2)若tanβ=(2-
| 3 |
| α |
| 2 |
(1)因为α+2β=
,
∴tanβ=tan[(α+2β)-(α+β)]=
=
=
=1
由β为锐角,得到β=
.
(2)由α+2β=
得
+β=
,
∴tan(
+β)=
=tan
=
,
∵tanβ=(2-
)cot
即tan
tanβ=2-
∴tan
+tanβ=3-
,
于是tan
和tanβ是一元二次方程x2-(3-
)x+2-
=0的两根,
解得x1=1,x2=2-
.
若tan
=1,则α=90°与0<α<90°矛盾,舍去;
∴tan
=2-
,tanβ=1,
∴α=30°,β=45°,
故满足条件的α和β存在,且α=30°,β=45°.
| 2π |
| 3 |
∴tanβ=tan[(α+2β)-(α+β)]=
| tan(α+2β)-tan(α+β) |
| 1+tan(α+2β)tan(α+β) |
tan
| ||||
1+(2+
|
- 2
| ||
-2
|
由β为锐角,得到β=
| π |
| 4 |
(2)由α+2β=
| 2π |
| 3 |
| α |
| 2 |
| π |
| 3 |
∴tan(
| α |
| 2 |
tan
| ||
1-tan
|
| π |
| 3 |
| 3 |
∵tanβ=(2-
| 3 |
| α |
| 2 |
| α |
| 2 |
| 3 |
∴tan
| α |
| 2 |
| 3 |
于是tan
| α |
| 2 |
| 3 |
| 3 |
解得x1=1,x2=2-
| 3 |
若tan
| α |
| 2 |
∴tan
| α |
| 2 |
| 3 |
∴α=30°,β=45°,
故满足条件的α和β存在,且α=30°,β=45°.

练习册系列答案
相关题目
已知关于某设备的使用年限x与所支出的维修费用y(万元)有如下的统计资料:
若y与x为线性相关关系,其线性回归方程为
=
x+
所表示的直线一定经过定点 .
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
已知关于某设备的使用年限x与所支出的维修费用y(万元),有如下统计资料:
|
使用年限x |
2 |
3 |
4 |
5 |
6 |
|
维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若y对x呈线性相关关系,则回归直线方程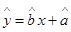 表示的直线一定过定点 .
表示的直线一定过定点 .