题目内容
若(a+b)⊥(2a-b),(a-2b)⊥(2a+b),试求a,b的夹角的余弦值.
解:由(a+b)⊥(2a-b),(a-2b)⊥(2a+b)有
![]()
即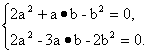
∴a2=![]() b2,|a|2=
b2,|a|2=![]() |b|2,|a|=
|b|2,|a|=![]() |b|.
|b|.
由2a2+a·b-b2=0,得
a·b=b2-2a2=|b|2-2|a|2=|b|2-2×![]() |b|2=-
|b|2=-![]() |b|2,
|b|2,
∴cosθ=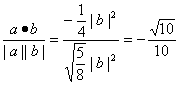 .
.
∴a,b的夹角的余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
若(a+b)⊥(2a-b),(a-2b)⊥(2a+b),试求a,b的夹角的余弦值.
解:由(a+b)⊥(2a-b),(a-2b)⊥(2a+b)有
![]()
即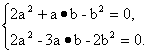
∴a2=![]() b2,|a|2=
b2,|a|2=![]() |b|2,|a|=
|b|2,|a|=![]() |b|.
|b|.
由2a2+a·b-b2=0,得
a·b=b2-2a2=|b|2-2|a|2=|b|2-2×![]() |b|2=-
|b|2=-![]() |b|2,
|b|2,
∴cosθ=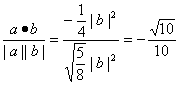 .
.
∴a,b的夹角的余弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案