题目内容
．(12分)飞机每飞行1小时的费用由两部分组成，固定部分为4900元，变动部分
（元）与飞机飞行速度
（千米∕小时）的函数关系式是
，已知甲乙两地的距离为
（千米）．
（1）试写出飞机从甲地飞到乙地的总费用
（元）关于速度（千米∕小时）的函数关系式；
（2）当飞机飞行速度为多少时，所需费用最少？
（元）与飞机飞行速度（千米∕小时）的函数关系式是，已知甲乙两地的距离为（千米）．（1）试写出飞机从甲地飞到乙地的总费用
（元）关于速度（千米∕小时）的函数关系式；（2）当飞机飞行速度为多少时，所需费用最少？
(1) 
(2)当飞机的飞行速度为700千米/小时时费用最小.
(2)当飞机的飞行速度为700千米/小时时费用最小.
本题考查了由函数模型建立目标函数，利用基本不等式求函数最值的问题，属于中档题．
（1）从甲地到乙地的飞行成本y（元）=每小时的燃料费用×时间+每小时其它费用×时间；
（2）由（1）求得函数表达式，用基本不等式可求得最小值
解：(1)每小时的费用为
，飞行时间为
小时
所以总费用关于速度的函数关系为
(2)
当且仅当
即
时上式等号成立. 所以当飞机的飞行速度为700千米/小时时费用最小.
（1）从甲地到乙地的飞行成本y（元）=每小时的燃料费用×时间+每小时其它费用×时间；
（2）由（1）求得函数表达式，用基本不等式可求得最小值
解：(1)每小时的费用为
，飞行时间为小时所以总费用
关于速度的函数关系为 (2)
当且仅当
即时上式等号成立. 所以当飞机的飞行速度为700千米/小时时费用最小.
练习册系列答案
相关题目
的解析式及其定义域；
在(0,1)内恰有一个解,则a的取值范围是( ) 
，则构造从集合
到集合
的映射，最多有（ ）
个
个
个
个
.则f(x)=( )
是奇函数，且
，若
，则
。
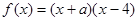为偶函数，则实数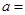
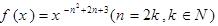的图像在
上单调递增，则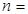
.