题目内容
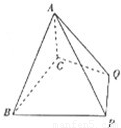
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.

(Ⅰ)若点G是AE的中点,求证:AC∥平面BDG;
(Ⅱ)试问点F在线段AB上什么位置时,二面角B-CE-F的余弦值为![]() .
.
答案:
解析:

解析:
(Ⅰ)证明:设![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,易知
,易知![]() 为
为![]() 的中位线,故
的中位线,故![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() . 4分
. 4分
(Ⅱ)解:如图,建立空间直角坐标系![]() ,在
,在![]() 中,斜边
中,斜边![]() ,
,![]() ,得
,得![]() ∴
∴![]() ,
,![]() ,
,![]() .设
.设![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由 ,即
,即 ,
, ,取
,取![]() ,得
,得![]() .
.
而平面![]() 的法向量
的法向量![]() ,∴由题得
,∴由题得 ,
,
即 ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
∴当点![]() 在线段
在线段![]() 的中点时,二面角
的中点时,二面角![]() 的余弦值为
的余弦值为![]() . 14分
. 14分


练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
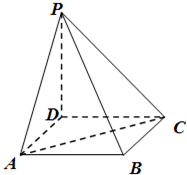 如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=
如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=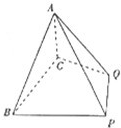 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
 BC,AB=AC=
BC,AB=AC=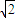 B.
B.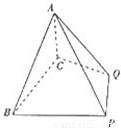
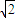 BC,AB=AC=
BC,AB=AC=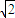 B.
B.