题目内容
(本小题满分12分)
已知点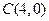 和直线
和直线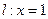 ,作
,作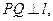 垂足为Q,且
垂足为Q,且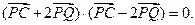
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线m与点P的轨迹交于两点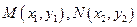
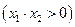 点
点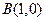 ,若
,若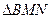 的面积为
的面积为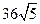 ,求直线
,求直线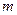 的方
的方 程.
程.
已知点
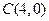 和直线
和直线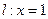 ,作
,作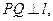 垂足为Q,且
垂足为Q,且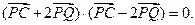
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线m与点P的轨迹交于两点
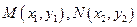
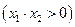 点
点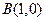 ,若
,若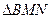 的面积为
的面积为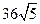 ,求直线
,求直线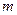 的方
的方 程.
程.解:(Ⅰ) 由已知 知
知 .
.
所以
设 ,代入上式得
,代入上式得
平方整理得. …………………………………………………………4分
…………………………………………………………4分
(Ⅱ)由题意可知设直线 的斜率不为零,且
的斜率不为零,且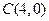 恰为双曲线的右焦点,
恰为双曲线的右焦点,
设直线 的方程为
的方程为 ,
,
由 …………………………………6分
…………………………………6分
若 ,则直线
,则直线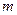 与双曲线只有一个交点,这与
与双曲线只有一个交点,这与 矛盾,故
矛盾,故 .
.
由韦达定理可得
 …………………………8分
…………………………8分


 ………………………………10分
………………………………10分
故直线 的方程为
的方程为 .………………………………12分
.………………………………12分
 知
知 .
.所以

设
 ,代入上式得
,代入上式得
平方整理得.
 …………………………………………………………4分
…………………………………………………………4分(Ⅱ)由题意可知设直线
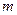 的斜率不为零,且
的斜率不为零,且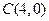 恰为双曲线的右焦点,
恰为双曲线的右焦点,设直线
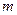 的方程为
的方程为 ,
,由
 …………………………………6分
…………………………………6分若
 ,则直线
,则直线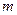 与双曲线只有一个交点,这与
与双曲线只有一个交点,这与 矛盾,故
矛盾,故 .
.由韦达定理可得

 …………………………8分
…………………………8分

 ………………………………10分
………………………………10分故直线
 的方程为
的方程为 .………………………………12分
.………………………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点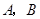 两点.
两点. 满足
满足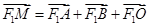 (其中
(其中 为坐标原点),求点
为坐标原点),求点 轴上是否存在定点
轴上是否存在定点 ,使
,使 ·
· 为常数?若存在,求出点
为常数?若存在,求出点


 面积的最小值。
面积的最小值。 上,按图示方式剪下两个正方形,其中
上,按图示方式剪下两个正方形,其中 ,∠
,∠
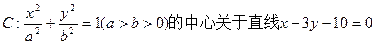 的对称点落在直线
的对称点落在直线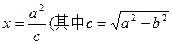 )上,且椭圆C的离心率为
)上,且椭圆C的离心率为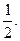
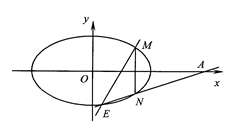
 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为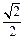 的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程; 是等腰三角形,
是等腰三角形, ,则以
,则以 为焦点且过点
为焦点且过点 的双曲线的离心率为( )
的双曲线的离心率为( )



 作垂直于
作垂直于 轴的垂线交曲线
轴的垂线交曲线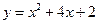 于点
于点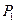 ,又过点
,又过点 轴于点
轴于点 ,记点
,记点 的对称点为
的对称点为 ;……;依此类推.若数列
;……;依此类推.若数列 的各项分别为点列
的各项分别为点列 的横坐标,且
的横坐标,且 ,则
,则 .
.
 是双曲线
是双曲线 的两个焦点,
的两个焦点, 是双曲线上的一点,且
是双曲线上的一点,且 ,则
,则 的面积等于
的面积等于


