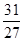题目内容
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+ ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )
| A.[1,2] |
B. |
C. |
| D.(0,2] |
C
解析

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知直线y=mx与函数 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.(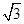 ,4) ,4) |
B.( ,+∞) ,+∞) |
C.( ,5) ,5) |
D.(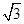 , , ) ) |
已知 其导函数
其导函数 的图象如图,则函数
的图象如图,则函数 的极小值是( )
的极小值是( )
A. |
B. |
C. |
| D.c |
为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像上所有的点( )
的图像上所有的点( )
| A.向左平移3个单位长度,再向上平移1个单位长度 |
| B.向右平移3个单位长度,再向上平移1个单位长度 |
| C.向左平移3个单位长度,再向下平移1个单位长度 |
| D.向右平移3个单位长度,再向下平移1个单位长度 |
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
A. |
B.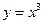 |
C. |
D. |
函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则函数
,则函数 的零点为( )
的零点为( )
| A.2 |
B. |
| C.3 |
| D.0 |
已知f(x)是定义在R上的以3为周期的偶函数,若f(1)<1,f(5)=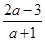 ,则实数a的取值范围为()
,则实数a的取值范围为()
| A.-1<a<4 | B.-2<a<1 | C.-1<a<2 | D.-1<a<0 |