题目内容
已知k为正常数,方程x2-kx+u=0有两个正数解x1,x2.(1)求实数u的取值范围;
(2)求使不等式(
 -x1) (
-x1) ( -x2)≥(
-x2)≥( -
- )2恒成立的k的取值范围.
)2恒成立的k的取值范围.
【答案】分析:(1)根据方程x2-kx+u=0有两个正数解x1,x2.可建立不等式组,从而得解;
(2)先利用韦达定理,将左边表示成实数u的式子,利用导数法研究其最小值,从而解决恒成立问题.
解答:解:(1)由于方程x2-kx+u=0有两个正数解x1,x2.
所以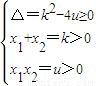 …(3分)解得0<u≤
…(3分)解得0<u≤ ,
,
即实数u的取值范围是(0,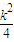 ];…(6分)
];…(6分)
(2)( -x1) (
-x1) (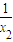 -x2)=x1x2+
-x2)=x1x2+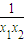 -
-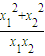 =u-
=u-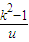 +2.
+2.
令f (u)=u-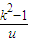 +2(u>0),所以f′(u)=1+
+2(u>0),所以f′(u)=1+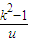 ,…(8分)
,…(8分)
(i)若k≥1,因为0<u≤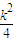 ,所以f′(u)>0,从而f (u)在(0,
,所以f′(u)>0,从而f (u)在(0,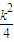 ]为增函数,所以
]为增函数,所以
u-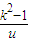 +2≤f (
+2≤f (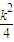 )=
)=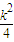 -
-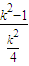 +2=(
+2=(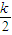 -(
-(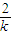 )2,
)2,
即(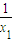 -x1) (
-x1) (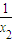 -x2)≥((
-x2)≥((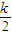 -(
-(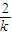 )2不恒成立.…(10分)
)2不恒成立.…(10分)
(ii)若0<k<1,由f′(u)=1+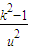 =0,得u=
=0,得u=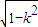 ,
,
当u∈(0,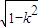 ),f′(u)<0;当u∈(
),f′(u)<0;当u∈(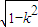 ,+∞),f′(u)>0,
,+∞),f′(u)>0,
所以函数f (u)在(0,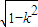 ]上递减,在[
]上递减,在[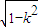 ,+∞)上递增,…(12分)
,+∞)上递增,…(12分)
要使函数f (u)在(0,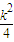 ]上恒有f (u)≥f (
]上恒有f (u)≥f (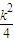 ),必有
),必有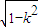 ≥
≥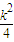 ,即k4+16 k2-16≤0,…(14分)
,即k4+16 k2-16≤0,…(14分)
解得0<k≤2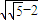 .综上,k的取值范围是(0,2
.综上,k的取值范围是(0,2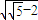 ].…(16分)
].…(16分)
点评:本题以方程为载体,考查方程根问题,考查恒成立的处理,关键是进行分类讨论,利用导数研究函数的最小值.
(2)先利用韦达定理,将左边表示成实数u的式子,利用导数法研究其最小值,从而解决恒成立问题.
解答:解:(1)由于方程x2-kx+u=0有两个正数解x1,x2.
所以
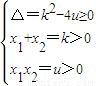 …(3分)解得0<u≤
…(3分)解得0<u≤ ,
,即实数u的取值范围是(0,
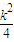 ];…(6分)
];…(6分)(2)(
 -x1) (
-x1) (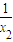 -x2)=x1x2+
-x2)=x1x2+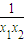 -
-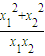 =u-
=u-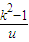 +2.
+2.令f (u)=u-
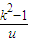 +2(u>0),所以f′(u)=1+
+2(u>0),所以f′(u)=1+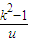 ,…(8分)
,…(8分)(i)若k≥1,因为0<u≤
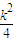 ,所以f′(u)>0,从而f (u)在(0,
,所以f′(u)>0,从而f (u)在(0,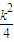 ]为增函数,所以
]为增函数,所以u-
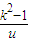 +2≤f (
+2≤f (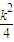 )=
)=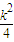 -
-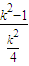 +2=(
+2=(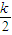 -(
-(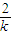 )2,
)2,即(
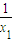 -x1) (
-x1) (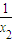 -x2)≥((
-x2)≥((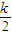 -(
-(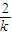 )2不恒成立.…(10分)
)2不恒成立.…(10分)(ii)若0<k<1,由f′(u)=1+
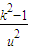 =0,得u=
=0,得u=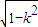 ,
,当u∈(0,
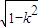 ),f′(u)<0;当u∈(
),f′(u)<0;当u∈(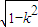 ,+∞),f′(u)>0,
,+∞),f′(u)>0,所以函数f (u)在(0,
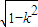 ]上递减,在[
]上递减,在[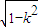 ,+∞)上递增,…(12分)
,+∞)上递增,…(12分)要使函数f (u)在(0,
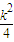 ]上恒有f (u)≥f (
]上恒有f (u)≥f (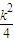 ),必有
),必有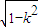 ≥
≥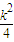 ,即k4+16 k2-16≤0,…(14分)
,即k4+16 k2-16≤0,…(14分)解得0<k≤2
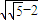 .综上,k的取值范围是(0,2
.综上,k的取值范围是(0,2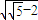 ].…(16分)
].…(16分)点评:本题以方程为载体,考查方程根问题,考查恒成立的处理,关键是进行分类讨论,利用导数研究函数的最小值.

练习册系列答案
相关题目
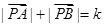 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;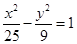 与椭圆
与椭圆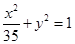 有相同的焦点;
有相同的焦点;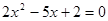 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;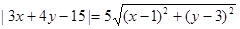 ,则点P的轨迹是一条直线.
,则点P的轨迹是一条直线.