题目内容
(2008•南京模拟)已知k为正常数,方程x2-kx+u=0有两个正数解x1,x2.
(1)求实数u的取值范围;
(2)求使不等式(
-x1) (
-x2)≥(
-
)2恒成立的k的取值范围.
(1)求实数u的取值范围;
(2)求使不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
分析:(1)根据方程x2-kx+u=0有两个正数解x1,x2.可建立不等式组,从而得解;
(2)先利用韦达定理,将左边表示成实数u的式子,利用导数法研究其最小值,从而解决恒成立问题.
(2)先利用韦达定理,将左边表示成实数u的式子,利用导数法研究其最小值,从而解决恒成立问题.
解答:解:(1)由于方程x2-kx+u=0有两个正数解x1,x2.
所以
…(3分)解得0<u≤
,
即实数u的取值范围是(0,
];…(6分)
(2)(
-x1) (
-x2)=x1x2+
-
=u-
+2.
令f (u)=u-
+2(u>0),所以f′(u)=1+
,…(8分)
(i)若k≥1,因为0<u≤
,所以f′(u)>0,从而f (u)在(0,
]为增函数,所以
u-
+2≤f (
)=
-
+2=(
-(
)2,
即(
-x1) (
-x2)≥((
-(
)2不恒成立.…(10分)
(ii)若0<k<1,由f′(u)=1+
=0,得u=
,
当u∈(0,
),f′(u)<0;当u∈(
,+∞),f′(u)>0,
所以函数f (u)在(0,
]上递减,在[
,+∞)上递增,…(12分)
要使函数f (u)在(0,
]上恒有f (u)≥f (
),必有
≥
,即k4+16 k2-16≤0,…(14分)
解得0<k≤2
.综上,k的取值范围是(0,2
].…(16分)
所以
|
| k2 |
| 4 |
即实数u的取值范围是(0,
| k2 |
| 4 |
(2)(
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1x2 |
| x12+x22 |
| x1x2 |
| k2-1 |
| u |
令f (u)=u-
| k2-1 |
| u |
| k2-1 |
| u |
(i)若k≥1,因为0<u≤
| k2 |
| 4 |
| k2 |
| 4 |
u-
| k2-1 |
| u |
| k2 |
| 4 |
| k2 |
| 4 |
| k2-1 | ||
|
| k |
| 2 |
| 2 |
| k |
即(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
(ii)若0<k<1,由f′(u)=1+
| k2-1 |
| u2 |
| 1-k2 |
当u∈(0,
| 1-k2 |
| 1-k2 |
所以函数f (u)在(0,
| 1-k2 |
| 1-k2 |
要使函数f (u)在(0,
| k2 |
| 4 |
| k2 |
| 4 |
| 1-k2 |
| k2 |
| 4 |
解得0<k≤2
|
|
点评:本题以方程为载体,考查方程根问题,考查恒成立的处理,关键是进行分类讨论,利用导数研究函数的最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
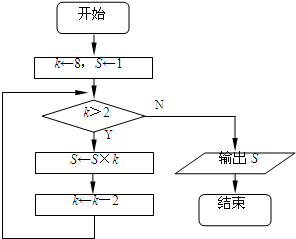 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是