题目内容
在△ABC中,三内角A,B,C所对的边分别为a,b,c,若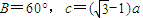 .
.(1)求角C的大小;
(2)已知当x∈R时,函数f(x)=sinx(cosx+asinx)的最大值为1,求a的值.
【答案】分析:(1)由题意A=120°-C,代入 得
得 展开求C
展开求C
(2)利用恒等变换公式对f(x)=sinx(cosx+asinx)化简得到f(x)= +
+ sin(2x-θ),再由最大值为1,建立方程求出a
sin(2x-θ),再由最大值为1,建立方程求出a
解答:解:(1)由题意若 ,可变为
,可变为 ,即
,即
∴
整理得
可得tanC=1,C=
(2)f(x)=sinx(cosx+asinx)= sin2x+
sin2x+ (1-cos2x)=
(1-cos2x)= +
+ sin(2x-θ),tanθ=a
sin(2x-θ),tanθ=a
∵函数f(x)=sinx(cosx+asinx)的最大值为1
∴ +
+ =1,
=1,
∴a+ =2,解得a=
=2,解得a=
点评:本题考查三角函数的最值,解题的关键是把三角函数的解析式转化为函数y=Asin(ωx+φ)的形式,再由三角函数的性质确定函数的最值,此类题一般有两种类型,一是求最值,一是由最值求参数,本题是第二类.
 得
得 展开求C
展开求C(2)利用恒等变换公式对f(x)=sinx(cosx+asinx)化简得到f(x)=
 +
+ sin(2x-θ),再由最大值为1,建立方程求出a
sin(2x-θ),再由最大值为1,建立方程求出a解答:解:(1)由题意若
 ,可变为
,可变为 ,即
,即
∴

整理得

可得tanC=1,C=

(2)f(x)=sinx(cosx+asinx)=
 sin2x+
sin2x+ (1-cos2x)=
(1-cos2x)= +
+ sin(2x-θ),tanθ=a
sin(2x-θ),tanθ=a∵函数f(x)=sinx(cosx+asinx)的最大值为1
∴
 +
+ =1,
=1,∴a+
 =2,解得a=
=2,解得a=
点评:本题考查三角函数的最值,解题的关键是把三角函数的解析式转化为函数y=Asin(ωx+φ)的形式,再由三角函数的性质确定函数的最值,此类题一般有两种类型,一是求最值,一是由最值求参数,本题是第二类.

练习册系列答案
相关题目