题目内容
三个正数a、b、c成等比数列,则lga、lgb、lgc是( )
| A.等比数列 |
| B.既是等差又是等比数列 |
| C.等差数列 |
| D.既不是等差又不是等比数列 |
由三个正数a、b、c成等比数列,则b2=ac,
所以lgb2=lgac,即2lgb=lga+lgc.
也就是lgb-lga=lgc-lgb.
所以,lga、lgb、lgc是等差数列.
故选C.
所以lgb2=lgac,即2lgb=lga+lgc.
也就是lgb-lga=lgc-lgb.
所以,lga、lgb、lgc是等差数列.
故选C.

练习册系列答案
相关题目
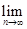
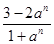 的值是 .
的值是 .