题目内容
若一次函数f(x)=mx+n有一个零点是2,则函数g(x)=nx2+mx的零点是
0和
| 1 |
| 2 |
0和
.| 1 |
| 2 |
分析:由一次函数f(x)=mx+n有一个零点是2,可得2m+n=0.∴n=-2m.(m≠0).代入函数g(x)=nx2+mx=-2mx2+mx=mx(-2x+1),即可得出其零点.
解答:解:∵一次函数f(x)=mx+n有一个零点是2,∴2m+n=0.∴n=-2m.(m≠0).
则函数g(x)=nx2+mx=-2mx2+mx=mx(-2x+1),
令g(x)=0,解得x=0或
.
∴函数g(x)的零点是0或
.
故答案为0或
.
则函数g(x)=nx2+mx=-2mx2+mx=mx(-2x+1),
令g(x)=0,解得x=0或
| 1 |
| 2 |
∴函数g(x)的零点是0或
| 1 |
| 2 |
故答案为0或
| 1 |
| 2 |
点评:本题考查了函数的零点的求法,属于基础题.

练习册系列答案
相关题目
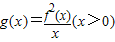 的值域为 .
的值域为 .