题目内容
下列命题:①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈(
 ),则f(sin θ)>f(cos θ);
),则f(sin θ)>f(cos θ);②若锐角α,β满足cos α>sin β,则α+β<
 ;
;③若f(x)=2cos2
 -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;④要得到函数y=sin
 的图象,只需将y=sin
的图象,只需将y=sin 的图象向右平移
的图象向右平移 个单位,
个单位,其中真命题是 (把你认为所有正确的命题的序号都填上).
【答案】分析:对于①,联系偶函数和增函数得到函数在[0,1]上为减函数后再解;
对于②,cos α>sin β要化成同名三角函数;
③f(x)=2cos2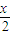 -1=cosx,
-1=cosx,
④函数y=sin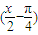 的系数
的系数 要引起特别注意.
要引起特别注意.
解答:解:①由已知可得函数在[0,1]上为减函数,
且由于θ∈(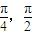 )⇒1>sinθ>cosθ>0,
)⇒1>sinθ>cosθ>0,
故有f(sinθ)<f(cosθ),
故①错;
②由已知角的范围可得:cosα>sinβ=cos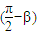 ⇒α<
⇒α<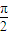 -β⇒α+β<
-β⇒α+β<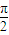 ,
,
故②正确;③错,
易知f(x)=cosx,其周期为2π,
故应有f(x)=f(x+2π)恒成立,④错,应向右平移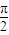 个单位得到.
个单位得到.
故答案为②
点评:本题是一道综合题,考查了函数的性质和三角函数中的二倍角公式以及三角函数图象的变换等.
对于②,cos α>sin β要化成同名三角函数;
③f(x)=2cos2
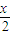 -1=cosx,
-1=cosx,④函数y=sin
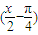 的系数
的系数 要引起特别注意.
要引起特别注意.解答:解:①由已知可得函数在[0,1]上为减函数,
且由于θ∈(
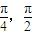 )⇒1>sinθ>cosθ>0,
)⇒1>sinθ>cosθ>0,故有f(sinθ)<f(cosθ),
故①错;
②由已知角的范围可得:cosα>sinβ=cos
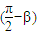 ⇒α<
⇒α<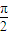 -β⇒α+β<
-β⇒α+β<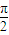 ,
,故②正确;③错,
易知f(x)=cosx,其周期为2π,
故应有f(x)=f(x+2π)恒成立,④错,应向右平移
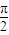 个单位得到.
个单位得到.故答案为②
点评:本题是一道综合题,考查了函数的性质和三角函数中的二倍角公式以及三角函数图象的变换等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
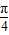 ,
,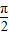 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);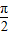 ;
;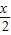 -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;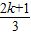 πx-
πx-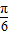 )(k∈N*)在区间[a,a+3]上的值
)(k∈N*)在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则k可以取2和3.
出现的次数不小于4次,又不多于8次,则k可以取2和3.