Question

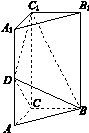
 [2012·课标全国卷] 如图1－4，三棱柱ABC－A₁B₁C₁中，侧棱垂直底面，∠ACB＝90°，AC＝BC＝AA₁，D是棱AA₁的中点．

(1)证明：平面BDC₁⊥平面BDC；

(2)平面BDC₁分此棱柱为两部分，求这两部分体积的比．

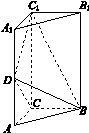
图1－4

Answer 1

解：(1)证明：由题设知BC⊥CC₁，BC⊥AC，CC₁∩AC＝C，所以BC⊥平面ACC₁A₁.

又DC₁⊂平面ACC₁A₁，所以DC₁⊥BC.

由题设知∠A₁DC₁＝∠ADC＝45°，所以∠CDC₁＝90°，即DC₁⊥DC.又DC∩BC＝C，所以DC₁⊥平面BDC.又DC₁⊂平面BDC₁，故平面BDC₁⊥平面BDC.

(2)设棱锥B－DACC₁的体积为V₁，AC＝1.由题意得

V₁＝××1×1＝.

又三棱柱ABC－A₁B₁C₁的体积V＝1，

所以(V－V₁)∶V₁＝1∶1.

故平面BDC₁分此棱柱所得两部分体积的比为1∶1.