题目内容
在平面坐标系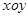 中,直线
中,直线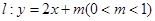 与圆
与圆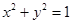 相交于
相交于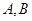 ,(
,(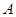 在第一象限)两个不同的点,且
在第一象限)两个不同的点,且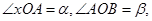 则
则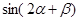 的值是 ( )
的值是 ( )
A.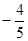 | B. | C.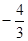 | D.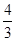 |
A
解析试题分析:如图,则 ,∴
,∴ ,即
,即 ,
,
∴ ,由题意得,
,由题意得, ,
,
又∵ ,∴
,∴ ,
,
∴ .
.
考点:三角恒等变形的具体运用.

练习册系列答案
相关题目
 是( ).
是( ).
| A.奇函数 |
| B.偶函数 |
| C.既是奇函数也是偶函数 |
| D.既不是奇函数也不是偶函数 |
过平面区域 内一点
内一点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为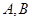 ,记
,记 ,则当
,则当 最小时
最小时 的值为( )
的值为( )
A.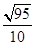 | B. | C. | D. |
已知 ,那么
,那么 的值是( )
的值是( )
A. | B. | C. | D. |
在 中,若
中,若 分别为
分别为 的对边,且
的对边,且 ,则有( )
,则有( )
| A.a、c、b成等比数列 | B.a、c、b成等差数列 |
| C.a、b、c成等差数列 | D.a、b、c成等比数列 |
 的值等于( )
的值等于( )
A. | B. | C. | D. |
已知tan(α﹣β)= ,且α,β∈(0,π),则2α﹣β=( )
,且α,β∈(0,π),则2α﹣β=( )
A. | B. | C. | D. |
若cosθ+sinθ=- ,则cos(
,则cos( -2θ)的值为( )
-2θ)的值为( )
A. | B.- | C. | D.- |
已知角 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的非负半轴重合,终边在直线
轴的非负半轴重合,终边在直线 上,则
上,则 等于( )
等于( )
A. | B. | C. | D. |