Question

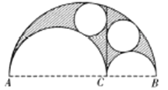
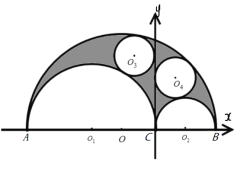
【题目】在一个半圆中有两个互切的内切半圆,由三个半圆弧围成曲边三角形,作两个内切半圆的公切线把曲边三角形分隔成两块,阿基米德发现被分隔的这两块的内切圆是同样大小的,由于其形状很像皮匠用来切割皮料的刀子,他称此为“皮匠刀定理”,如图,若,则阴影部分与最大半圆的面积比为（ ）

A.B.

C.D.

Answer 1

【答案】B

【解析】

设,则,,建立平面直角坐标系,分别求出各点坐标,,,,,设两个小圆圆心,,则根据圆与圆内切,解得.同理,得,由圆与圆内切,得,于是阿基米德“皮匠刀定理”得证.再对面积求比即可.

解：设,则,,建立如图所示的坐标系,

,,,,设,,

则,得,所以,

由圆与圆内切,得,解得.

同理,得,

由圆与圆内切,得,解得,

于是阿基米德“皮匠刀定理”得证.

,

所以.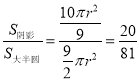

故选：B