题目内容
已知二次函数 满足条件
满足条件 ,当
,当 时
时 恒成立.
恒成立.
(1)求 ;
;
(2)求 的解析式;
的解析式;
(3)若 ,且
,且 ,求证:
,求证: .
.
【答案】
(1)∵
∴当 时.
时.  .
.
∴ .
.
(2)由(1)知 , 又
, 又 ∴
∴
从而 , 又
, 又 时,
时, 恒成立.
恒成立.
即 故
故 ∴
∴
∴ 而
而 ∴
∴
∴ ∴
∴ . ∴
. ∴ .
.
(3)∵
∴ ∴
∴ (当且仅当
(当且仅当 时取等号)
时取等号)
∴ ∴
∴ .
.
又 .
.
∴ (当且仅当
(当且仅当 时取等号)
时取等号)

练习册系列答案
相关题目
 满足条件
满足条件 ,及
,及 .
. 上的最大和最小值.
上的最大和最小值.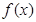 满足条件
满足条件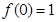 ,及
,及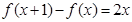 .
.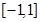 上的最值.
上的最值.